31/03/2022
Διερεύνηση της κλίσης της ευθείας
Δημιουργοί / ΣυντελεστέςΕΚΠΑ/ΕΤΤ - δημιουργία
Συνοπτική περιγραφήΤο σενάριο στοχεύει να εμπλέξει μαθητές και μαθήτριες Α΄ Λυκείου στη διερεύνηση του ρόλου των παραμέτρων α και β και ειδικότερα της α στη γραφική παράσταση της συνάρτησης f(x)=αx+β. Οι μαθητές έχουν διαπραγματευθεί στο Γυμνάσιο τη γραφική παράσταση της ευθείας y=αx+β και εδώ καλούνται μέσα από συγκεκριμένες δραστηριότητες να περιγράψουν τις μεταβολές του α με διαφορετικούς τρόπους και να χρησιμοποιήσουν αυτές τις περιγραφές στην ερμηνεία της μοντελοποίησης καταστάσεων
Γνωστικό/ά αντικείμενο/α – γνωστική/ές περιοχή/έςΜαθηματικά > Άλγεβρα > Η συνάρτηση y=αχ+β
Το συγκεκριμένο σενάριο αφορά την Άλγεβρα, συγκεκριμένα τη γνωστική περιοχή των συναρτήσεων και πιο ειδικά τη γραμμική συνάρτηση.
Θέμα (τα)Διερεύνηση της έννοιας της κλίσης και χειρισμός σχετικών μοντέλων.
Γλώσσα (ες) σεναρίουελληνικά
Οι μαθητές στο Γυμνάσιο έχουν διαπραγματευθεί τη γραφική παράσταση της ευθείας y=αx+β, εδώ θα διερευνήσουν το ρόλο που έχουν οι παράμετροι α και β, και κυρίως η α, στη γραφική παράσταση της συνάρτησης f(x)=αx+β και θα κληθούν να περιγράψουν τι επιφέρει η μεταβολή της α στην ευθεία. Μέσα από κατάλληλες δραστηριόττες και αξιοποιώντας αντίστοιχο ψηφιακό υλικό οι μαθητές θα παρατηρήσουν πως μεταβάλλεται η γραφική παράσταση όταν μεταβάλλεται η ανεξάρτητη μεταβλητή, σε διαφορετικά πλαίσια και θα αναζητήσουν το ρόλο της παραμέτρου α σε αυτές τις μεταβολές. Στόχος είναι να συνδέσουν την κλίση της ευθείας με τη γωνία τριγώνου, αλλα και με άλλα μαθηματικά αντικείμενα (π.χ. συντεταγμένες σημείων), μέσα από την παρατήρηση των παραπάνω μεταβολών και στη συνέχεια να εμπλακούν με επίλυση προβλημάτων και κυρίως χειρισμό σχετικών μοντέλων και περιγραφή τους με την έννοια της κλίσης.
Παιδαγωγική προσέγγιση και στρατηγικέςΟι μαθητές και οι μαθήτριες έχοντας στη διάθεση τους ψηφιακό υλικό που προέρχεται από μικροπειράματα του εμπλουτισμένου σχολικού βιβλίου προσπαθούν να απαντήσουν στα ερωτήματα που τίθενται στις δραστηριότητες των μικροπειραμάτων. Με πειραματισμό προσπαθούν να καταλήξουν στις σωστές απαντήσεις, ταυτόχρονα το λογισμικό του δίνει κάποιες βοήθειες αν οι μαθητές κρίνουν ότι είναι χρήσιμες. Ο ρόλος του εκπαιδευτικού είναι να υποστηρίζει τις προσπάθειες των μαθητών και να τους παροτρύνει να πειραματιστούν με τα εργαλεία του λογισμικού, παράλληλα υποστηρίζει τους πιο αδύναμους μαθητές με κατάλληλο τρόπο. Συντονίζει τη συζήτηση τόσο στο πλαίσιο της ομάδας όσο και στο πλαίσιο της ολομέλειας. Η υποστήριξη του εκπαιδευτικού θα έχει και στοιχεία διαφοροποίησης της διδασκαλίας.
γενικό λύκειο
ΤάξηΑ' Λυκείου
Γλώσσα στοχευόμενου κοινούελληνικά, αγγλικά
Εκτιμώμενος χρόνος υλοποίησης σεναρίου (διάρκεια)μικρή διάρκεια: έως 3 ώρες
Τρεις (03) διδακτικές ώρες.
Χώρος υλοποίησηςΠροτείνεται η εργασία σε ομάδες των τριών ατόμων στο εργαστήριο πληροφορικής όπου η κάθε ομάδα χρησιμοποιεί έναν υπολογιστή. Ωστόσο, το σενάριο μπορεί να υλοποιηθεί και με σύγχρονη εξ΄ αποστάσεως διδασκαλία. Τότε οι ομάδες προτείνεται να είναι μεγαλύτερες (π.χ πενταμελείς), ώστε ο εκπαιδευτικός να μπορεί να επικοινωνήσει αποτελεσματικά με όλες τις ομάδες.
Ενορχήστρωση τάξης Οργάνωση τάξης / διδασκαλίαςΣτην περίπτωση της δια ζώσης υλοποίησης του σεναρίου οι ομάδες των μαθητών προτείνεται να είναι τριμελείς.
Στην περίπτωση που η διδασκαλία γίνει εξ΄ αποστάσεως σύγχρονα, τότε οι ομάδες προτείνεται να είναι πενταμελείς και να συνεργάζονται σε διαφορετικό «δωμάτιο» η κάθε ομάδα. Ο εκπαιδευτικός χρειάζεται να παρακολουθεί και να επισκέπτεται τα «δωμάτια συνεργασίας» των ομάδων.
Ρόλοι μαθητών & εκπαιδευτικώνΗ περίπτωση της δια ζώσης διδασκαλίας.
Σε κάθε τριμελή ομάδα οι ρόλοι είναι διακριτοί. Ένας μαθητής χειρίζεται τον υπολογιστή, ένας κρατάει σημειώσεις και ο τρίτος έχει την ευθύνη να διαχειρίζεται και να οργανώνει την επικοινωνία της ομάδας με τον εκπαιδευτικό και την υπόλοιπη τάξη, στην ολομέλεια (πώς θα γίνει, ποιος θα θέσει κάθε ερώτημα, κτλ). Μπορούν οι ρόλοι να εναλλάσσονται μεταξύ των μελών της ομάδας, από ώρα σε ώρα διδασκαλίας.
Ο εκπαιδευτικός, αρχικά χωρίζει τους μαθητές και τις μαθήτριες σε ομάδες με τρόπο τέτοιο ώστε όλες οι ομάδες να έχουν καλή συνεργασία και λειτουργία. Για παράδειγμα, ένα κριτήριο μπορεί να είναι τα μέλη της κάθε ομάδας να έχουν ξανασυνεργαστεί ώστε να μην χρειάζεται χρόνος προσαρμογής. Χωρίς να αποκλείεται σε μια «ειδική συνθήκη» που σταθμίζει ο εκπαιδευτικός να είναι σκόπιμο να συνεργαστούν για πρώτη φορά μαθητές/τριες μεταξύ τους.
Κατά τη διάρκεια της υλοποίησης ο εκπαιδευτικός παρατηρεί όλες τις ομάδες και παρεμβαίνει με στόχο πάντα την εμπλοκή των μελών της κάθε ομάδας στη διερεύνηση που έχει δοθεί, επίσης θέτει ερωτήματα και προβληματισμούς τόσο στην ολομέλεια όσο και σε κάθε ομάδα ανάλογα με την εξέλιξη και ροή των δραστηριοτήτων.
Κρίσιμος είναι ο ρόλος του εκπαιδευτικού ως προς τη διαφοροποίηση της διδασκαλίας. Η δραστηριότητα σε όλες τις ομάδες θα είναι αρχικά η ίδια αλλά στην πορεία θα διαφοροποιείται για διάφορους λόγους, όπως π.χ. επειδή κάποια ομάδα ολοκληρώνει γρήγορα τις δραστηριότητες θα πρέπει να έχει κάτι να ασχοληθεί όσο οι άλλες ομάδες βρίσκονται στη φάση υλοποίησης, ο εκπαιδευτικός θα πρέπει λοιπόν να έχει προνοήσει να υπάρχουν διαθέσιμα επιπλέον ερωτήματα ώστε να τεθούν προς συζήτηση και επίλυση στις ομάδες που ολοκληρώνουν την αρχική δραστηριότητα. Ο εκπαιδευτικός θα υποστηρίζει τις διαφορετικές κατευθύνσεις της διερεύνησης, σε κάθε ομάδα αφήνοντας να διερευνώνται τα διαφορετικά ερωτήματα. Επίσης, θα φροντίζει ώστε κάθε ομάδα να έχει το χρόνο που της χρειάζεται για να ολοκληρώσει τη διερεύνησή της, χωρίς να απαιτείται όλες οι ομάδες να προχωρούν με την ίδια ταχύτητα σε όλες τις φάσεις του σεναρίου.
Η περίπτωση της σύγχρονης εξ αποστάσεως διδασκαλίας.
Οι τροποποιήσεις που προτείνονται είναι οι εξής:
- Οι ομάδες να είναι πενταμελείς και σε κάθε ομάδα θα υπάρχει ένας presenter ώστε να μοιράζει την οθόνη του στα υπόλοιπα μέλη της ομάδας, το ρόλο αυτό καλό είναι να τον αναλαμβάνει μαθητής ο οποίος έχει πρόσβαση σε Η/Υ και όχι σε φορητή συσκευή (tablet, smartphone) για λόγους εύκολης χρήσης.
- Ο εκπαιδευτικός θα πρέπει να έχει φροντίσει το ψηφιακό υλικό να εύκολα προσβάσιμο στους μαθητές είτε μέσω links είτε μέσω υπηρεσιών νέφους.
- Ο ρόλος του εκπαιδευτικού αλλάζει κυρίως ως προς τη ρύθμιση των συνθηκών συνεργασίας μεταξύ των μαθητών/τριών, π.χ. οι «χρόνοι» που απαιτούνται ενδεχομένως επιμηκύνονται λόγω της εξ΄ αποστάσεως επικοινωνίας. Επίσης προτείνεται οι ομάδες να επανέρχονται στην ολομέλεια για συζήτηση και ανταλλαγή απόψεων μια φορά σε κάθε διδακτική ώρα, που να συνοψίζει τη συζήτηση (και όχι περισσότερες).
- Η επικοινωνία του εκπαιδευτικού τόσο με την κάθε ομάδα αλλά και με όλες τις ομάδες μπορεί να γίνει εύκολα με χρήση γραπτών μνημάτων μέσω του chat.
Από πλευράς Μαθηματικών χρειάζεται οι μαθητές και οι μαθήτριες να γνωρίζουν τι ονομάζουμε συνάρτηση αλλά και τι γραφική παράσταση συνάρτησης. Επίσης, να μπορούν στοιχειωδώς να αντλούν πληροφορίες από το γράφημα, όπως συντεταγμένες σημείων.
Από πλευράς χρήσης του ψηφιακού εργαλείου Geogebra οι μαθητές είναι χρήσιμο να γνωρίζουν στοιχειωδώς τις λειτουργίες του.
Απαιτούμενα βοηθητικά υλικά και εργαλείαΤο λογισμικό GeoGebra http://geogebra.org και τα Σχολικά Διαδραστικά Βιβλία http://ebooks.edu.gr/.
Στην περίπτωση της δια ζώσης διδασκαλίας: Η/υ ή tablets με σύνδεση στο διαδίκτυο, προβολικό ή διαδραστικός πίνακας, τετράδια, μολύβια, γεωμετρικά όργανα (κανόνας, τρίγωνο, διαβήτης), σχολικό βιβλίο Μαθηματικών Α΄ Λυκείου).
Στην περίπτωση της δια ζώσης διδασκαλίας: Τα ίδια χωρίς το προβολικό ή το διαδραστικό πίνακα. Επιπλέον χρειάζεται λογισμικό σύγχρονης εξ αποστάσεως επικοινωνίας και μικρόφωνο.
Απαιτούμενη προετοιμασίαΣε αυτό το σενάριο χρησιμοποιούνται μικροπειράματα του σχολικού βιβλίου, τα οποία είναι αναρτημένα στο Φωτόδεντρο / Σχολικά Διαδραστικά Βιβλία. Άρα, μπορούν να ανοίξουν διαδικτυακά και από τα παιδιά στους υπολογιστές τους ή τα tablets τους. Ωστόσο, προτείνεται ο εκπαιδευτικός να έχει αποθηκεύσει στον υπολογιστή του όλα τα μικροπειράματα που πρόκειται να χρησιμοποιηθούν, για να αντιμετωπίσει την περίπτωση οποιασδήποτε ενδεχόμενης δυσλειτουργίας κατά τη διάρκεια του μαθήματος.
Στην περίπτωση που οι μαθητές και οι μαθήτριες δεν έχουν ξαναχρησιμοποιήσει το εκπαιδευτικό λογισμικό GeoGebra θα μπορούσε ο εκπαιδευτικός να διαθέσει μια διδακτική ώρα στην αρχή του σχολικού έτους ώστε να γίνει μια γνωριμία με τις βασικές λειτουργίες και εργαλεία του.
Οι μαθητές και οι μαθήτριες:
>> Να περιγράφουν τη μορφή της γραφική παράσταση της f(x)=αx+β για τα συγκεκριμένες τιμές των παραμέτρων α και β.
>> Να περιγράφουν την κλίση της γραφικής παράστασης της f(x)=αx+β, για διαφορετικές τιμές του α, με βάση διαφορετικά μοντέλα (τρίγωνο, σχέση μεταξύ των συντεταγμένων σημείων της ευθείας).
>> Να χρησιμοποιούν την έννοια της κλίσης για τη μοντελοποίηση καταστάσεων και την επίλυση προβλημάτων.
ΔεξιότητεςΟι μαθητές και οι μαθήτριες:
>> Απαντούν σε ερωτήματα μετά από διερεύνηση.
>> Πειραματίζονται για να πετύχουν τις κατασκευές που ζητούνται.
>> Παίρνουν αποφάσεις ως προς τη λύση που θα παρουσιάσουν στις άλλες ομάδες.
>> Τεκμηριώνουν τις επιλογές τους σε συζήτηση στην ολομέλεια.
Στάσεις, συμπεριφορές, αξίεςΟι μαθητές και οι μαθήτριες:
>> Αναζητούν λύση ακολουθώντας τη «κουλτούρα του δημιουργού».
>> Καταβάλουν προσπάθεια για συναινέσεις στην ομάδα.
Παιδαγωγική προσέγγιση και στρατηγικέςΓια να επιτευχθούν τα προσδοκώμενα μαθησιακά αποτελέσματα ακολουθείται η προσέγγιση της μάθησης μέσα από τον πειραματισμό, που δίνει την ευκαιρία στα παιδιά να διατυπώσουν εικασίες τις οποίες επιβεβαιώνουν ή απορρίπτουν μέσα από τη χρήση του λογισμικού. Η πρόκληση ξεκινάει από συγκεκριμένα μικροπειράματα που θέτουν το σχετικά προβλήματα. Από την άλλη τα ερωτήματα που τίθενται μπορούν να απαντηθούν με διαφορετικούς τρόπους. Έτσι, τα παιδιά θέτουν τα ίδια επιμέρους ερωτήματα και μαθαίνουν να διερευνούν και να ψάχνουν λύσεις, να κάνουν υποθέσεις και εικασίες.
Σε αυτό το σημείο οι λειτουργικότητες του ψηφιακού εργαλείου, η σύνδεση μεταξύ δυναμικών αναπαραστάσεων (η χρήση των δρομέων), η ανατροφοδότηση που παρέχει στα παιδιά (αλλάζουν τιμές στο δρομέα που επηρεάζει την παράμετρο α και βλέπουν πως αλλάζει η θέση της ευθείας στο επίπεδο) είναι παράμετροι που υποστηρίζουν τον πειραματισμό, τη διερεύνηση και την κουλτούρα του δημιουργού. Επίσης, κρίσιμος είναι ο ρόλος του εκπαιδευτικού στην ενίσχυση, οργάνωση και διευκόλυνση της επικοινωνίας μεταξύ των παιδιών της ίδιας ομάδας αλλά και στην ολομέλεια. Η επικοινωνία αυτή είναι αναγκαία ώστε να πάρουν αποφάσεις εντός της ομάδας, να διασφαλίσουν την συναίνεση εντός της ομάδας για να προχωρήσουν, να εξηγήσουν τις επιμέρους επιλογές τους, να τεκμηριώσουν τη στρατηγική που ακολούθησαν, να αξιολογήσουν τις προσπάθειες των συμμαθητών τους, να συνδέσουν τη μαθηματική γνώση με τις πρακτικές τους.
Σε όλες τις φάσεις του σεναρίου οι μαθητές και οι μαθήτριες ανοίγουν ένα μικροπείραμα του σχολικού διαδραστικού βιβλίου. Σε κάθε μικροπείραμα υπάρχουν ενσωματωμένα ερωτήματα στα οποία οι μαθητές και οι μαθήτριες καλούνται να απαντήσουν, παράλληλα υπάρχει βοήθεια ώστε όταν κάποια ομάδα έχει εγκλωβιστεί και δεν μπορεί να προχωρήσει ο εκπαιδευτικός τους προτείνει να αξιοποιήσουν αυτή τη δυνατότητα.
Αρχικά, ο εκπαιδευτικός χωρίζει τους μαθητές σε ομάδες και τους αναθέτει ρόλους (ή τους ζητά να αναλάβουν ρόλους) χειριστή ψηφιακού εργαλείου, εκείνου που είναι υπεύθυνος για τις σημειώσεις της ομάδας και του υπεύθυνου επικοινωνίας της ομάδας. Αυτό γίνεται κάθε φορά που αρχίζει νέα διδακτική ώρα. Στη συνέχεια τους ζητά να ανοίξουν το πρώτο μικροπείραμα (παρακάτω), να και να προσπαθήσουν να απαντήσουν στα ερωτήματα που περιέχει. Στη συνέχεια συνεχίζουν με το δεύτερο μικροπείραμα. Μετά την αντιμετώπιση των ερωτημάτων κάθε μικροπειράματος γίνεται συζήτηση στην ολομέλεια και αποφασίζονται, με συζήτηση τα κριτήρια που θα κριθεί ποιες είναι οι κατάλληλες απαντήσεις.
Στη Φάση 1 του σεναρίου οι μαθητές έχουν στη διάθεσή τους έτοιμο αρχείο GeoGebra με ενσωματωμένα ερωτήματα που προκαλούν πειραματισμό και διερεύνηση και καλούνται να απαντήσουν σε αυτά. Ο στόχος στη φάση αυτή είναι να νοηματοδοτήσουν το ρόλο που έχουν οι παράμετροι α και β στη γραφική παράσταση της συνάρτησης f(x)=αx+β και συγκεκριμένα οι τιμές της παραμέτρου α με την κλίση της ευθείας y=αx+β. Αυτός ο στόχος μπορεί να επιτευχθεί μέσα από την εμπλοκή με το μικροπείραμα http://photodentro.edu.gr/v/item/ds/8521/1757
Στη συνέχεια στο παρακάτω μικροπείραμα http://photodentro.edu.gr/v/item/ds/8521/1758 καλούνται να απαντήσουν σε ερωτήματα που έχουν να κάνουν με τις μεταβολές των τιμών της συνάρτησης και πως αυτές επηρεάζονται από τις τιμές των παραμέτρων α και β, κυρίως της α και τα συμπεράσματά τους τα επιβεβαιώνουν, παίρνοντας ανατροφοδότηση από το μικροπείραμα.
Στη Φάση 2 του σεναρίου οι μαθητές και οι μαθήτριες χρησιμοποιούν την έννοια της κλίσης για να συζητήσουν για ένα πρόβλημα που τους τίθεται, καθώς χειρίζονται ένα μοντέλο που βασίζεται στην γραμμική συνάρτηση.
http://photodentro.edu.gr/v/item/ds/8521/1759
Η δομή της ροής του σεναρίου είναι αυτή που ακολουθεί (ο χρόνος που υπολογίζεται για κάθε φάση δίνεται ως ένα μέτρο σύγκρισης μεταξύ των φάσεων, τελείως ενδεικτικά).
«Τι αλλάζει, όταν πειράζουμε την τιμή του α; Του β;»
Συνοπτική περιγραφήΑρχικά οι μαθητές και οι μαθήτριες ανοίγουν το μικροπείραμα που βρίσκεται στον παρακάτω σύνδεσμο:
http://photodentro.edu.gr/v/item/ds/8521/1757
και προσπαθούν καλούνται, από το μικροπείραμα, να υπολογίσουν την κλίση της ευθείας. Η έννοια της κλίσης μπορεί να είναι γνωστή ως «ο αριθμός α». Όμως εδώ, μπορούν να δουν τι επιφέρει η αλλαγή του α στη γραφική παράσταση:
>> μέσα από την εμφάνιση του τριγώνου ABC που αλλάζει μαζί με την ευθεία καθώς μεταβάλλονται τα α και β,
>> και κυρίως από τις συνδεδεμένες αναπαραστάσεις και το δυναμικό χειρισμό τους (τιμή του α και μεταβολές στην ευθεία).
Έτσι, έχουν ευκαιρίες να «συμπληρώσουν» την εικόνα τους για την έννοια της κλίσης, παρατηρώντας τις αλλαγές στο τρίγωνο αυτό και να συνδέσουν την κλίση της ευθείας με την κλίση μιας γωνίας του τριγώνου.
Στη συνέχεια τους δίνεται το μικροπείραμα που βρίσκεται στον παρακάτω σύνδεσμο:
http://photodentro.edu.gr/v/item/ds/8521/1758
Εδώ, οι μαθητές καλούνται να απαντήσουν σε παρόμοια ερωτήματα, σχετικά με την κλίση. Όμως σε αυτό το μικροπείραμα δεν είναι ορατό το τρίγωνο αυτό που μεταβάλλεται μαζί με την ευθεία. Έτσι, είναι ενδιαφέρουσα η συζήτηση που μπορεί να προκληθεί και να φανεί αν αυτή θα συνεχιστεί με αναφορά στο τρίγωνο του προηγούμενου μικροπειράματος.
Διδακτικοί στόχοι / Προσδοκώμενα μαθησιακά αποτελέσματα>> Να περιγράφουν τη μορφή της γραφική παράσταση της f(x)=αx+β για τα συγκεκριμένες τιμές των παραμέτρων α και β.
>> Να περιγράφουν την κλίση της γραφικής παράστασης της f(x)=αx+β, για διαφορετικές τιμές του α, με βάση διαφορετικά μοντέλα (τρίγωνο, σχέση μεταξύ των συντεταγμένων σημείων της ευθείας).
>> Απαντούν σε ερωτήματα μετά από διερεύνηση.
>> Τεκμηριώνουν τις επιλογές τους σε συζήτηση στην ολομέλεια.
Είδος δραστηριότητας>>Αρχικά οι μαθητές και οι μαθήτριες πειραματίζονται με τις τιμές των δρομέων α και β χρησιμοποιώντας το πρώτο μικροπείραμα και προσπαθούν να συνδέσουν την κλίση της ευθείας με την τιμή του α, κάνουν υπολογισμούς και ελέγχουν τις εικασίες τους.
Μια χρήσιμη ερώτηση που θα μπορούσε να θέσει ο εκπαιδευτικός είναι «μπορείτε να περιγράψετε τι βλέπετε να συμβαίνει, καθώς αλλάζει το α;» Εδώ, μπορεί να υπάρξουν περιγραφές της κίνησης της ευθείες, αλλά και άλλες με χρήση της σχέσης των μηκών των κάθετων πλευρών του τριγώνου BC και AC. Είναι χρήσιμο να υποστηριχθεί από τον εκπαιδευτικό η συζήτηση μεταξύ των μαθητών γύρω από όλα αυτά (βλέπε τις παρακάτω εικόνες).

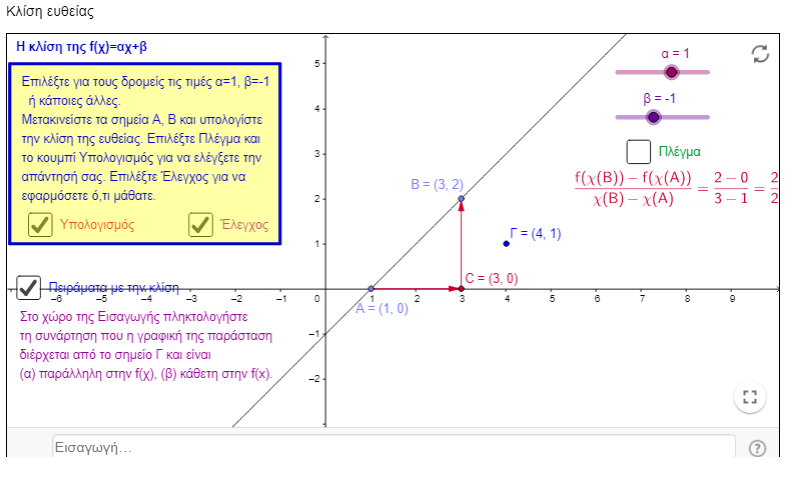
>> Με το δεύτερο μικροπείραμα που υλοποιείται κατά τη διάρκεια της 1ης φάσης οι μαθητές πραγματοποιούν πειράματα με τα μήκη δύο ευθυγράμμων τμημάτων και παρατηρούν πώς αυτά μεταβάλλονται καθώς αλλάζουν τις τιμές στους δρομείς α και β. Στη συνέχεια πραγματοποιούν πειράματα με τις συντεταγμένες των άκρων των ευθυγράμμων τμημάτων. Άρα, από το προηγούμενο μικροπείραμα έχουν «μείνει» μόνο οι συντεταγμένες των πλευρών του τριγώνου.
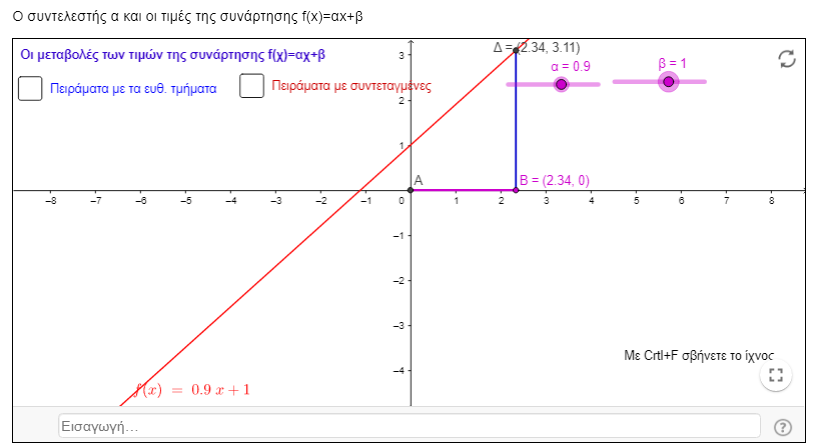
Εδώ, ο εκπαιδευτικός μπορεί να προκαλέσει συζήτηση σχετικά με τη διαφορά των δύο περιπτώσεων, θέτοντας ερωτήματα όπως: «Γιατί δεν υπάρχει το τρίγωνο εδώ; Ποια είναι η κλίση της ευθείας και πώς σχετίζεται με το τρίγωνο; Χρειάζεται να σχεδιάζουμε το τρίγωνο;»
>> Στο τέλος της διερεύνησης και της συζήτησής τους, μπορούν να πάρουν ανατροφοδότηση σε επίπεδο τυπικών μαθηματικών (βλέπε παρακάτω εικόνα).

2 διδακτικές ώρες
Τεχνική/ές διδασκαλίαςΙσχύουν τα αναφερόμενα στην παράγραφο «Παιδαγωγική προσέγγιση και στρατηγικές».
ΠηγέςΦωτόδεντρο: http://photodentro.edu.gr/lor/
«Πλακόστρωση αυλής»
Συνοπτική περιγραφήΒασίζεται στο ομώνυμο μικροπείραμα που βρίσκεται στον παρακάτω σύνδεσμο.
http://photodentro.edu.gr/v/item/ds/8521/1759
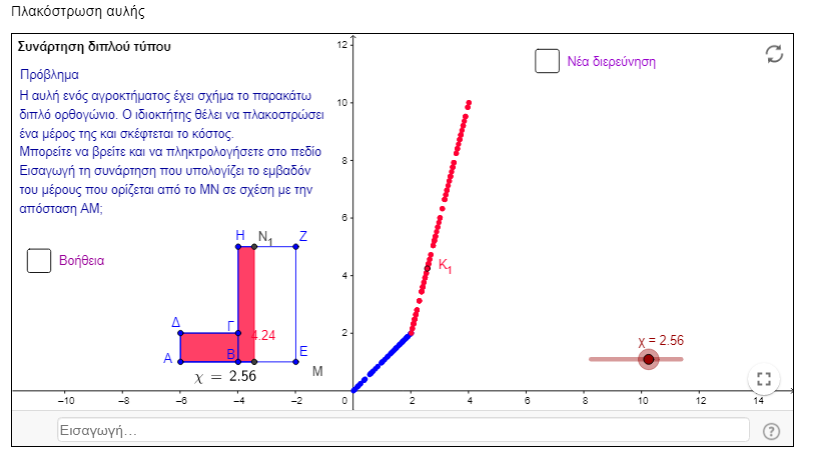
Στόχος είναι οι μαθητές να πειραματιστούν με τις τιμές του δρομέα x και να ανακαλύψουν τον τύπο που δίνει σε κάθε περίπτωση το εμβαδόν του αντίστοιχου τμήματος της αυλής. Μπορούν να κάνουν πειράματα και με τα εργαλεία του λογισμικού, όπως το ενεργό ίχνος ενός σημείου να αποκαλύψουν τη γραφική παράσταση της συνάρτησης που ψάχνουν και στη συνέχεια να αναζητήσουν τον τύπο της.
Διδακτικοί στόχοι / Προσδοκώμενα μαθησιακά αποτελέσματα>> Να χρησιμοποιούν την έννοια της κλίσης για τη μοντελοποίηση καταστάσεων και την επίλυση προβλημάτων.
>> Απαντούν σε ερωτήματα μετά από διερεύνηση.
>> Πειραματίζονται για να πετύχουν τις κατασκευές που ζητούνται.
>> Παίρνουν αποφάσεις ως προς τη λύση που θα παρουσιάσουν στις άλλες ομάδες.
>> Τεκμηριώνουν τις επιλογές τους σε συζήτηση στην ολομέλεια.
Είδος δραστηριότηταςΜέσω του προβλήματος που διατυπώνεται οι μαθητές και οι μαθήτριες χρειάζεται να κατασκευάσουν και να διατυπώσουν ένα μαθηματικό μοντέλο, π.χ. τον τύπο της συνάρτησης που υπολογίζει το εμβαδόν της αυλής για τις διάφορες τιμές του x (μήκος ΑΜ). Παράλληλα, μέσω του χειρισμού του μοντέλου στο μικροπείραμα μπορούν να βλέπουν συνδεδεμένες:
>> τη μεταβολή του x και
>> το μεταβλητό σημείο που αντιστοιχεί στα ζεύγη τιμών (x, εμβαδόν αυλής).
Επίσης, βλέπουν να σχηματίζεται σταδιακά το ίχνος του σημείου αυτού.
Αρχικά οι μαθητές/τριες εργάζονται σε ομάδες όπως στην πρώτη φάση. Ο εκπαιδευτικός χρειάζεται να υποστηρίξει, στη συνέχεια, τη συζήτηση στην ολομέλεια για να συζητηθούν διαφορετικές στρατηγικές και προσεγγίσεις, οι μαθητές/τριες να χρησιμοποιήσουν στα επιχειρήματά τους την έννοια της κλίσης (όπως έχει σχηματιστεί μετά τη φάση 1) για να εξηγήσουν πώς λειτουργεί το μοντέλο που χειρίζονται στο μικροπείραμα και τελικά να απαντήσουν στην πρόκληση που τους τίθεται.
Εκτιμώμενη διάρκεια1 διδακτική ώρα
Τεχνική/ές διδασκαλίαςΙσχύουν τα αναφερόμενα στην παράγραφο «Παιδαγωγική προσέγγιση και στρατηγικές».
Επιπροσθέτως ο εκπαιδευτικός θα πρέπει να είναι σε ετοιμότητα να ανταποκριθεί σε ανάγκες διαφοροποιημένης διδασκαλίας.
ΠηγέςΦωτόδεντρο: http://photodentro.edu.gr/lor/
Εναλλακτικά στη φάση 2, μπορεί να αξιοποιηθεί το μικροπείραμα:
http://photodentro.edu.gr/v/item/ds/8521/1880
Οι μαθητές καλούνται να υπολογίσουν τη συνάρτηση που δίνει το εμβαδόν του συγκεκριμένου τριγώνου και έχουν στη διάθεσή τους πληροφορίες που τους προσφέρει το λογισμικό όπως μέρος της γραφικής παράστασης αυτής της συνάρτησης που ψάχνουν αλλά και πλούσια βοήθεια.
Με το συγκεκριμένο μικροπείραμα οι μαθητές και οι μαθήτριες καλούνται να βρουν ένα μαθηματικό μοντέλο που να αντιστοιχεί στη συνάρτηση x (δηλ. AM) και του εμβαδού του τριγώνου (βλέπε εικόνα).
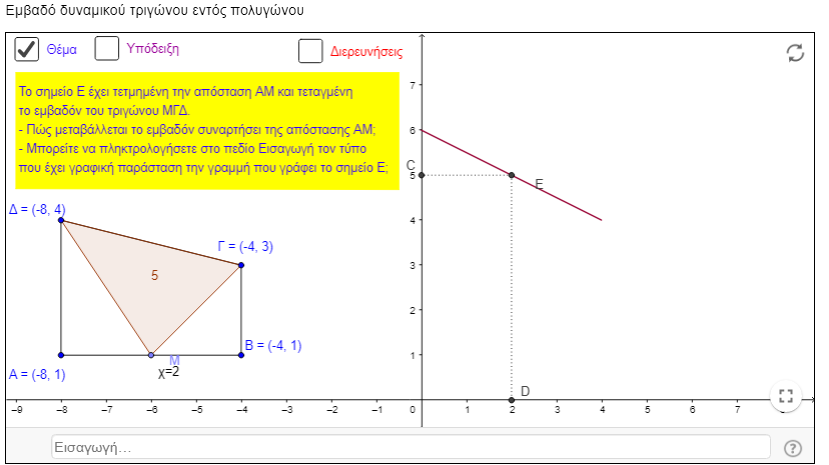
Οι μαθητές και μαθήτριες μετακινούν σημείο Μ που αποτελεί μια κορυφή ενός τριγώνου και έτσι μεταβάλλεται το εμβαδόν του τριγώνου, προσπαθούν να βρουν τον τύπο αυτής ενώ παράλληλα έχουν την πληροφορία για τη γραφικής της παράσταση.
Για την αποτίμηση του σεναρίου προτείνεται ο εκπαιδευτικός να κρατάει σημειώσεις που, εκτός από τη φάση της αξιολόγησης, θα τον βοηθήσουν να παρακολουθήσει τη διδασκαλία και την πορεία της μάθησης και να επανασχεδιάζει κατά τη διάρκεια της εφαρμογής, από φάση σε φάση του σεναρίου.
Συνοδευτικό υλικό
| Όνομα αρχείου | Περιγραφή | Τύπος αρχείου | Μέγεθος αρχείου |
|---|---|---|---|
| Picture1.png | Εικόνα 1 | image/png | 30 KB |
| Picture2.png | Εικόνα 2 | image/png | 68 KB |
| Picture3.png | Εικόνα 3 | image/png | 39 KB |
| Picture4.png | Εικόνα 4 | image/png | 156 KB |
| Picture5.png | Εικόνα 5 | image/png | 53 KB |
| Picture6.png | Εικόνα 6 | image/png | 50 KB |