19/07/2021
Προγραμματίζουμε παραλληλόγραμμα
Δημιουργοί / ΣυντελεστέςΕΚΠΑ/ΕΤΤ - δημιουργία
Συνοπτική περιγραφήΤο σενάριο στοχεύει να εμπλέξει μαθητές και μαθήτριες 12-15 ετών στη διερεύνηση και τη χρήση των ιδιοτήτων των παραλληλογράμμων. Ειδικότερα, για να πετύχουν τα ζητούμενα, δηλαδή την κατασκευή γενικευμένων σχημάτων που διατηρούν τις ιδιότητες παραλληλογράμμου, τα παιδιά θα εκφράσουν με αλγεβρικό τρόπο ιδιότητες που δηλώνουν τη σχέση μεταξύ των γωνιών αυτών των σχημάτων και άλλες που δηλώνουν τη σχέση των πλευρών τους. Στη συνέχεια θα τις χρησιμοποιήσουν σε προγράμματα για να κατασκευάσουν τα ζητούμενα σχήματα. Πρόκειται για μια διαδικασία που θα γίνει από τα παιδιά σε κύκλους πειραματισμού-εικασιών-ελέγχου των εικασιών-αναθεώρησης, 5-6 ωρών, εμπλέκοντάς τα σε αυθεντική μαθηματική δραστηριότητα.
Γνωστικό/ά αντικείμενο/α – γνωστική/ές περιοχή/έςΜαθηματικά > Γεωμετρία > Παραλληλόγραμμα
Μαθηματικά > Άλγεβρα
Το συγκείμενο το σεναρίου έχει ως αφετηρία τη Γεωμετρία και τις ιδιότητες παραλληλογράμμων. Ωστόσο, η δραστηριότητα που προκαλεί συσχετίζεται με την επίτευξη μαθησιακών αποτελεσμάτων στη θεματική της άλγεβρας (αλγεβρική έκφραση, χρήση γενικευμένων αριθμών), καθώς οι μαθητές/τριες χρειάζεται να εκφράσουν με αλγεβρικό τρόπο γεωμετρικές ιδιότητες για να τις χρησιμοποιήσουν.
Θέμα (τα)Θέμα: «Προγραμματισμός για το σχεδιασμό επίπεδων σχημάτων».
Γλώσσα (ες) σεναρίουελληνικά
Συνήθως, οι ιδιότητες παραλληλογράμμων αποτελούν μέρος των σχολικών μαθηματικών ακόμα και πριν την ηλικία των 12 ετών σαν ένα σετ κανόνων ή σαν μια λίστα γνώσεων που προστίθεται σε όσα γνωρίζουν ως τότε τα παιδιά. Αργότερα, κυρίως σε τάξεις μετά τα 15 έτη έρχονται οι έννοιες της ιδιότητας και του κριτηρίου μαζί με την ανάγκη της χρήσης ιδιοτήτων και κριτηρίων σε αποδείξεις. Π.χ. για τις ιδιότητες συνήθως λέμε το εξής: «αν γνωρίζουμε ότι ένα σχήμα είναι ρόμβος μπορούμε να χρησιμοποιήσουμε όλες τις ιδιότητες του ρόμβου». Για τα κριτήρια, από την άλλη, λέμε ότι «αν θέλουμε να αποδείξουμε ότι ένα σχήμα είναι ρόμβος χρειάζεται να τεκμηριώσουμε την ισχύ ενός συγκεκριμένου σετ ιδιοτήτων (κριτήρια), η τεκμηρίωση των οποίων μας επιτρέπει στο εξής να θεωρούμε το σχήμα αυτό ρόμβο.» Ενδεχομένως οι μαθητές αναρωτιούνται: «Γιατί, όμως είναι συγκεκριμένο το «σετ των ιδιοτήτων» που χρειάζεται να τεκμηριώσω; Γιατί δε χρειάζεται να τεκμηριώσω όλες τις ιδιότητες του ρόμβου;»
Προσπαθώντας να κατασκευάσουν π.χ. ένα γενικευμένο παραλληλόγραμμο, δηλαδή ένα παραλληλόγραμμο που ενώ μεταβάλλεται διατηρεί τις ιδιότητές του, οι μαθητές/τριες χρησιμοποιούν γεωμετρικές ιδιότητες, όπως «οι απέναντι πλευρές είναι ίσες» για να προγραμματίσουν μια οντότητα που μετακινείται σχεδιάζοντας ένα τέτοιο παραλληλόγραμμο. Για να χρησιμοποιήσουν τις ιδιότητες αυτές, χρειάζεται να τις εκφράσουν αλγεβρικά (π.χ. χρησιμοποιούν την ίδια μεταβλητή για το μήκος των πλευρών) και αυτό το πετυχαίνουν μέσα από συνεχείς κύκλους διερεύνησης και πειραματισμού: τρέχουν το πρόγραμμα, βλέπουν τι σχηματίζει, αναθεωρούν, το ξανατρέχουν. Έτσι, συμπεραίνουν σε κάθε περίπτωση, μέσα από τη διερεύνηση αυτή, ποιες ιδιότητες είναι αυτές που τελικά «δεσμεύουν» το σχήμα να είναι παραλληλόγραμμο.
Παιδαγωγική προσέγγιση και στρατηγικέςΟι μαθητές/τριες προσπαθώντας να απαντήσουν σε μια πρόκληση κατασκευής που τους τίθεται ξεκινούν τη διερεύνηση για να κατασκευάσουν το ζητούμενο. Το περιβάλλον στο οποίο δουλεύουν (η Χελωνόσφαιρα) τους δίνει τα μέσα να «μαστορέψουν» το πρόγραμμα και φτιάξουν βήμα-βήμα την κατασκευή τους, θέτοντας οι ίδιοι/ες επιμέρους ερωτήματα.
Αν και το αρχικό ερώτημα τίθεται από το έργο/μικροπείραμα, η προσέγγιση του σεναρίου ακολουθεί το πλαίσιο του Constructionism, καθώς τα παιδιά όχι μόνο θέτουν τα δικά τους επιμέρους ερωτήματα, αλλά μπορούν στη συνέχεια προχωρήσουν σε επεκτάσεις με δικές τους, σχετικές κατασκευές (π.χ. να φτιάξουν ρόμβο ή ένα μοτίβο από ρόμβους), εργάζονται σε μικρές ομάδες με ηλεκτρονικό υπολογιστή έχοντας το χρόνο να δοκιμάσουν τις ιδέες τους, ενθαρρύνονται από τον εκπαιδευτικό να κάνουν τις δικές τους κατασκευές και να τις ανταλλάξουν με τους συμμαθητές τους. Ο ρόλος του εκπαιδευτικού είναι να υποστηρίζει τα παιδιά να μάθουν μαστορεύοντας και να διευκολύνει αυτή τη πυκνή σε δημιουργία νοημάτων μαθησιακή δραστηριότητα, είτε με στοχευμένα ερωτήματα (όχι καθοδηγητικά), είτε φέρνοντας τη συζήτηση από τις ομάδες στην ολομέλεια, ανάλογα με την εξέλιξη της διερεύνησης. Η υποστήριξή του εκπαιδευτικού θα έχει και στοιχεία διαφοροποίησης της διδασκαλίας.
Σύμφωνα με το τρέχον πρόγραμμα σπουδών (ΠΣ) των Μαθηματικών, το σενάριο απευθύνεται σε παιδιά που παρακολουθούν την Α΄ τάξη του Γυμνασίου. Ωστόσο, μπορεί να απευθυνθεί σε όλες τις τάξεις του Γυμνασίου, ακόμα και χωρίς τροποποιήσεις, καθώς το θέμα των ιδιοτήτων και των κριτηρίων επανέρχεται στην Α΄ Λυκείου, χωρίς να συζητείται προηγουμένως στοχευμένα και εστιασμένα, και ως τότε είναι χρήσιμο να έχουν εμπλακεί οι μαθητές/τριες σε σχετική διερευνητική δραστηριότητα. Επιπλέον, σε επόμενες τάξεις από την Α΄ Γυμνασίου δίνεται η ευκαιρία για μεγαλύτερη εστίαση σε θέματα αλγεβρικής έκφρασης των ιδιοτήτων (όπως π.χ. στην Β΄ Γυμνασίου, στο πλαίσιο των συναρτήσεων).
Βαθμίδα Εκπαίδευσηςγυμνάσιο
Ηλικιακή ομάδαΑπό 12 Έως 15
Γλώσσα στοχευόμενου κοινούελληνικά, αγγλικά
Εκτιμώμενος χρόνος υλοποίησης σεναρίου (διάρκεια)μεσαία διάρκεια: από 4 ώρες έως 1 μήνα
Πέντε με έξι (5-6) διδακτικές ώρες.
Χώρος υλοποίησηςΙδανικό είναι οι μαθητές να εργάζονται ανά τρεις σε έναν ηλεκτρονικό υπολογιστή. Έτσι, προτείνεται το εργαστήριο υπολογιστών των σχολείου ως ο χώρος εφαρμογής του σεναρίου. Ωστόσο, μπορούν να βρεθούν λύσεις και εντός τάξης (με χρήση mobile-technology εφόσον το επιτρέπει ο εξοπλισμός του σχολείου). Σε εξ σύγχρονη αποστάσεως διδασκαλία προτείνεται ο χωρισμός σε λίγο μεγαλύτερες ομάδες (π.χ. πενταμελείς).
Ενορχήστρωση τάξης Οργάνωση τάξης / διδασκαλίαςΣτην περίπτωση που η διδασκαλία γίνει δια ζώσης, είτε με χρήση του εργαστηρίου υπολογιστών, είτε με χρήση mobile-technology (π.χ. tablets), οι ομάδες των παιδιών προτείνεται να είναι τριμελείς.
Στην περίπτωση που η διδασκαλία γίνει εξ αποστάσεως, με σύγχρονο τρόπο, τότε προτείνεται ο χωρισμός σε μεγαλύτερες ομάδες, π.χ. πενταμελείς, ώστε οι ομάδες να είναι λιγότερες και ο/η εκπαιδευτικός να προλαβαίνει να «μπαίνει στα δωμάτια» όλων των ομάδων.
Ρόλοι μαθητών & εκπαιδευτικώνΗ περίπτωση της δια ζώσης διδασκαλίας.
Σε κάθε τριάδα υπάρχουν ρόλοι των παιδιών, που καθορίζονται από τα ίδια: ο χειριστής του υπολογιστή/tablet, ο χρήστης του τετραδίου και ο συντονιστής. Ο χειριστής χρησιμοποιεί το ψηφιακό εργαλείο εκ μέρους της ομάδας, ο χρήστης του τετραδίου έχει την ευθύνη των σημειώσεων της ομάδας, ενώ ο συντονιστής έχει τη ευθύνη άλλων πόρων που αποφασίζει να χρησιμοποιήσει η ομάδα (π.χ. βιβλίο) και φροντίζει ώστε να μην «χάνεται το νήμα» μεταξύ των δύο και η ομάδα να δρα συντονισμένα. Όλοι είναι ισότιμοι ως προς την έκφραση γνώμης για τη διερεύνηση και ως προς την δυνατότητα να χρησιμοποιηθεί το ψηφιακό εργαλείο, ή το τετράδιο. Στην διάρκεια της διερεύνησης υπάρχει η δυνατότητα αλλαγής ρόλων στην ομάδα, εφόσον το αποφασίσουν τα παιδιά ή εφόσον το υποδείξει ο εκπαιδευτικός.
Ο εκπαιδευτικός έχει τον κρίσιμο ρόλο της φροντίδας να λειτουργήσει η τάξη παίρνοντας τις μαθησιακές ευκαιρίες που θα προκύψουν. Πιο συγκεκριμένα, φροντίζει να χωρίσει τις ομάδες με τρόπο λειτουργικό λαμβάνοντας υπόψη την καλύτερη λειτουργία τους (π.χ. να υπάρχει προοπτική να ακουστούν διαφορετικές απόψεις σε κάθε ομάδα, κτλ) προσέχοντας να μην έρθει κανένα παιδί σε δύσκολη θέση (π.χ. αν εκφραστεί έντονη δυσαρέσκεια για τη σύνθεση κάποιας ομάδας). Για παράδειγμα, μπορεί να δημιουργήσει ομάδες από την αρχή της σχολικής χρονιάς, οι οποίες να λειτουργούν σταθερά, χρησιμοποιώντας έναν τυχαίο τρόπο χωρισμού των ομάδων και κάνοντας σαφή και διάφανο στα παιδιά τον τρόπο αυτόν.
Κατά τη διάρκεια της διδασκαλίας, ο εκπαιδευτικός παρατηρεί τη διερεύνηση σε όλες τις ομάδες, τη συζήτηση μεταξύ των παιδιών και δίνει χρόνο να συζητήσουν μεταξύ τους. Παρεμβαίνει με τρόπο που να προκαλεί τη συζήτηση και τη διερεύνηση, π.χ. αν παρατηρήσει ότι ο προβληματισμός μιας ομάδας είναι σχετικός με κάτι που συζητούν οι υπόλοιπες, μπορεί να τον φέρει στην ολομέλεια ως ερώτημα ή θέμα προς συζήτηση χωρίς να το επιβάλει, διακόπτοντας για λίγο τις ομάδες και δίνοντας, αρχικά, το λόγο στην ομάδα που είχε αυτόν τον προβληματισμό. Στη συνέχεια οι ομάδες συνεχίζουν τη διερεύνηση.
Επίσης, κρίσιμος είναι ο ρόλος του εκπαιδευτικού ως προς τη διαφοροποίηση της διδασκαλίας. Η δραστηριότητα σε όλες τις ομάδες δε θα είναι η ίδια. Ο εκπαιδευτικός θα υποστηρίζει τις διαφορετικές κατευθύνσεις της διερεύνησης, σε κάθε ομάδα αφήνοντας να διερευνώνται τα διαφορετικά ερωτήματα. Επίσης, θα φροντίζει ώστε κάθε ομάδα να έχει το χρόνο που της χρειάζεται για να ολοκληρώσει τη διερεύνησή της, χωρίς να απαιτείται όλες οι ομάδες να προχωρούν με την ίδια ταχύτητα σε όλες τις φάσεις του σεναρίου. Μπορεί π.χ. τη δεύτερη ώρα να μη βρίσκονται όλες οι ομάδες στην ίδια φάση.
Άρα ο εκπαιδευτικός διευκολύνει, παρακολουθεί, υποστηρίζει, προκαλεί και συντονίζει τη δραστηριότητα των μαθητών/τριών και φροντίζει να διατηρεί την επικοινωνία και σε επίπεδο ολομέλειας όταν αυτό χρειάζεται.
Η περίπτωση της σύγχρονης εξ αποστάσεως διδασκαλίας.
Οι τροποποιήσεις που προτείνονται είναι οι εξής:
>> Οι ομάδες είναι πενταμελείς και οι ρόλοι των μαθητών είναι: ο χειριστής του ψηφιακού εργαλείου που το διαμοιράζει στα μέλη της ομάδας του (π.χ. με share screen), δύο χρήστες τετραδίου και δύο συντονιστές. Οι ρόλοι μπορούν να εναλλάσσονται, όπως πριν. Επίσης οι μαθητές/τριες όλων των ρόλων έχουν τη δυνατότητα να ανοίγουν το ψηφιακό εργαλείο στο υπολογιστή τους. Ωστόσο, αν θέλουν να δοκιμάσουν κάτι αφήνοντας για λίγο το ρόλο τους, αυτό θα πρέπει να συμφωνήσει με τον μαθητή/τρια που έχει τον αντίστοιχο ρόλο (π.χ. όταν ο ένας συντονιστής δοκιμάζει κάτι στον υπολογιστή του, τότε ο άλλος έχει αποκλειστικά το ρόλο του συντονιστή, ώστε να μη μείνει η ομάδα χωρίς συντονιστή) και η δοκιμή αυτή να έχει μικρή διαρκεία.
>> Ο ρόλος του εκπαιδευτικού δε διαφοροποιείται. Αλλάζει, αναγκαστικά ο τρόπος που δρα. Σε μια σύγχρονη εξ αποστάσεως συνεδρία διάρκειας μίας (1) διδακτικής ώρας, που οι μαθητές/τριες δουλεύουν σε ομάδες προτείνεται να μην διακόπτεται η λειτουργία των ομάδων για περισσότερο από μία φορά. Έτσι, ίσως είναι χρήσιμο να η επαναφορά της συζήτησης στην ολομέλεια να μη γίνεται τόσο συχνά. Αντιθέτως, ο εκπαιδευτικός μπορεί ο ίδιος να μεταφέρει έναν χρήσιμο προβληματισμό από μια ομάδα σε μια άλλη, εφόσον κρίνει ότι την αφορά.
>> Τέλος, στην ολομέλεια μπορεί να χρησιμοποιηθεί ο διαμοιρασμός οθόνης, άλλα και η ανταλλαγή προγραμμάτων με μηνύματα στη «συζήτηση» (chat) ώστε κάθε ομάδα να δείξει τι έκανε.
Απαιτήσεις εφαρμογής σεναρίου Προαπαιτούμενες γνώσεις των μαθητώνΑπό πλευράς Μαθηματικών χρειάζεται οι μαθητές/τριες να διακρίνουν ως σχήματα το τετράγωνο και το παραλληλόγραμμο, περισσότερο ως χωρικά αντικείμενα (δεν είναι απαραίτητο να μπορούν να τα ορίσουν ως γεωμετρικά αντικείμενα).
Από πλευράς χρήσης του ψηφιακού εργαλείου δεν είναι απαραίτητο οι μαθητές να γνωρίζουν προγραμματισμό ή να έχουν χρησιμοποιήσει ξανά τη Χελωνόσφαιρα. Στην περίπτωση που δεν την έχουν χρησιμοποιήσει, μπορεί να προηγηθεί ένα εισαγωγικό μάθημα βασικών λειτουργιών και προγραμματισμού (π.χ. να μπορούν να προγραμματίσουν και να σχηματίσουν δύο διαδοχικές μετατοπίσεις της οντότητας μεταξύ των οποίων υπάρχει στροφή, με μεταβλητή ή όχι).
Απαιτούμενα βοηθητικά υλικά και εργαλείαΤο λογισμικό Χελωνόσφαιρα http://etl.ppp.uoa.gr/malt2/ και τα Σχολικά Διαδραστικά Βιβλία http://ebooks.edu.gr/.
Στην περίπτωση της δια ζώσης διδασκαλίας: Η/υ ή tablets με σύνδεση στο διαδίκτυο, προβολικό ή διαδραστικός πίνακας, τετράδια, μολύβια, γεωμετρικά όργανα (κανόνας, τρίγωνο, διαβήτης), σχολικό βιβλίο Μαθηματικών Α΄ Γυμνασίου).
Στην περίπτωση της δια ζώσης διδασκαλίας: Τα ίδια χωρίς το προβολικό ή το διαδραστικό πίνακα. Επιπλέον χρειάζεται λογισμικό σύγχρονης εξ αποστάσεως επικοινωνίας και μικρόφωνο.
Απαιτούμενη προετοιμασίαΣε αυτό το σενάριο χρησιμοποιούνται μικροπειράματα του σχολικού βιβλίου, τα οποία είναι αναρτημένα στο Φωτόδεντρο / Σχολικά Διαδραστικά Βιβλία. Άρα, μπορούν να ανοίξουν διαδικτυακά και από τα παιδιά στους υπολογιστές τους ή τα tablets τους. Ωστόσο, προτείνεται ο εκπαιδευτικός να έχει αποθηκεύσει στον υπολογιστή του όλα τα μικροπειράματα που πρόκειται να χρησιμοποιηθούν, για να αντιμετωπίσει την περίπτωση οποιασδήποτε ενδεχόμενης δυσλειτουργίας κατά τη διάρκεια του μαθήματος.
Στην περίπτωση που οι μαθητές και οι μαθήτριες δεν έχουν ξαναπρογραμματίσει με τη Χελωνσόφαιρα στα παρελθόν, προτείνεται στον εκπαιδευτικό η προετοιμασία ενός έργου για την εξοικείωσή τους, του οποίου προσδοκώμενο μαθησιακό αποτέλεσμα είναι να μπορούν να φτιάξουν ένα πρόγραμμα της παρακάτω μορφής και να ενεργοποιήσουν τους μεταβολείς, περιγράφοντας τι κάνει ο καθένας:
ΓΙΑ :χ :θ
Μπροστά 100
Δεξιά :θ
Μπροστά :χ
ΤΕΛΟΣ
Οι μαθητές και οι μαθήτριες:
>> Χρησιμοποιούν την ίδια μεταβλητή για να εκφράσουν ότι θα πρέπει δύο ή περισσότερες ποσότητες να είναι ίσες.
>> Χρησιμοποιούν μεταβλητές για να εκφράσουν σχέσεις εξάρτησης, όπως της παραπληρωματικής γωνίας (180-φ).
>> Κατασκευάζουν στη Χελωνόσφαιρα γενικευμένο τετράγωνο και παραλληλόγραμμο.
>> Αναγνωρίζουν μοτίβα στην κατασκευή του τετραγώνου (π.χ. πηγαίνεις μπροστά :χ και δεξιά 90, 4 φορές) και του παραλληλογράμμου.
>> Χρησιμοποιούν αυτά τα μοτίβα στην κατασκευή τετραγώνου και παραλληλογράμμου, με εντολές επανάληψης.
>> Χρησιμοποιούν την έκφραση 180-φ, για να σχεδιάσουν τα παραπάνω σχήματα.
>> Ανακαλούν στρατηγικές κατασκευής σχημάτων και τις χρησιμοποιούν σε άλλες κατηγορίες σχημάτων.
>> Εξηγούν γιατί έχουν χρησιμοποιήσει μεταβλητές, με συγκεκριμένο τρόπο, σε κάθε ένα από τα παραπάνω προγράμματα.
>> Συνδέουν τη χρήση των μεταβλητών στα προγράμματα με τις ιδιότητες του τετραγώνου και του παραλληλογράμμου.
>> Αξιολογούν τα προγράμματα των συμμαθητών τους.
>> Δημιουργούν δικά τους σχήματα με δομικές λίθους τα προγράμματα τετραγώνου, παραλληλογράμμου που έχουν ήδη κατασκευάσει.
ΔεξιότητεςΟι μαθητές και οι μαθήτριες:
>> Διερευνούν διαφορετικές περιπτώσεις, ώστε να αντιμετωπίσουν το ερώτημα που τους τίθεται από το έργο.
>> Πειραματίζονται στη Χελωνόσφαιρα για να πετύχουν τις κατασκευές που ζητούνται.
>> Κάνουν εικασίες και υποθέσεις τις οποίες ελέγχουν στο περιβάλλον της Χελωνόσφαιρας.
>> Θέτουν επιμέρους ερωτήματα για να πετύχουν το ζητούμενο.
>> Θέτουν σχετικά ερωτήματα δικού τους ενδιαφέροντος.
>> Παίρνουν αποφάσεις ως προς τη λύση που θα παρουσιάσουν ανάμεσα στις προτεινόμενες στην ομάδα τους.
>> Τεκμηριώνουν τις επιλογές τους σε συζήτηση στην ολομέλεια.
Στάσεις, συμπεριφορές, αξίεςΟι μαθητές και οι μαθήτριες:
>> Δείχνουν ανοχή στην αμφισημία.
>> Αναζητούν λύση ακολουθώντας τη «κουλτούρα του δημιουργού».
>> Καταβάλουν προσπάθεια για συναινέσεις στην ομάδα.
Παιδαγωγική προσέγγιση και στρατηγικέςΓια να επιτευχθούν τα προσδοκώμενα μαθησιακά αποτελέσματα ακολουθείται η προσέγγιση του Constructionism, της μάθησης μέσα από το μαστόρεμα, που δίνει την ευκαιρία στα παιδιά να δημιουργήσουν νοήματα προσπαθώντας να πετύχουν κάτι που έχει αξία για τα ίδια. Η πρόκληση ξεκινάει από συγκεκριμένα μικροπειράματα που θέτουν το σχετικό μαθηματικό περικείμενο, καθώς είναι εστιασμένα. Από την άλλη τα ερωτήματα που τίθενται μπορούν να απαντηθούν με διαφορετικούς τρόπους. Έτσι, τα παιδιά θέτουν τα ίδια επιμέρους ερωτήματα και μαθαίνουν να διερευνούν και να ψάχνουν λύσεις, να κάνουν υποθέσεις και εικασίες χωρίς να είναι μονοσήμαντα ορισμένο το επόμενο βήμα.
Για να απαντήσουν στα ερωτήματα που τίθενται από το έργο ή θέτουν τα παιδιά, θα χρειαστεί να χρησιμοποιήσουν μεταβλητές για να εκφράσουν συγκεκριμένες ιδιότητες. Ο ρόλος του εκπαιδευτικού είναι να επισημάνει τη χρησιμότητα των μεταβλητών, χωρίς να καθοδηγήσει τα παιδιά, ώστε τα ίδια να αναγνωρίζουν μοτίβα, ιδιότητες, κτλ και να πειραματιστούν με τη χρήση των αλγεβρικών εκφράσεων σε κάθε πρόγραμμα. Από την εκτέλεση των προγραμμάτων θα αποφανθούν αν χρειάζεται να αλλάξουν κάτι (κουλτούρα δημιουργού). Σε αυτό το σημείο οι λειτουργικότητες του ψηφιακού εργαλείου, οι σύνδεση μεταξύ δυναμικών αναπαραστάσεων (η χρήση των μεταβολέων), η ανατροφοδότηση που παρέχει στα παιδιά (εκτελούν το πρόγραμμα και βλέπουν τι συμβαίνει) είναι παράμετροι που υποστηρίζουν τον πειραματισμό, τη διερεύνηση και την κουλτούρα του δημιουργού. Επίσης, κρίσιμος είναι ο ρόλος του εκπαιδευτικού στην ενίσχυση, οργάνωση και διευκόλυνση της επικοινωνίας μεταξύ των παιδιών της ίδιας ομάδας ή στην ολομέλεια. Η επικοινωνία αυτή είναι αναγκαία ώστε να πάρουν αποφάσεις εντός της ομάδας, να διασφαλίσουν την συναίνεση εντός της ομάδας για να προχωρήσουν, να εξηγήσουν τις επιμέρους επιλογές τους, να τεκμηριώσουν τη στρατηγική που ακολούθησαν, να αξιολογήσουν τις προσπάθειες των συμμαθητών τους, να συνδέσουν τη μαθηματική γνώση με τις πρακτικές τους.
Σε όλες τις φάσεις του σεναρίου οι μαθητές και οι μαθήτριες ανοίγουν ένα μικροπείραμα του σχολικού διαδραστικού βιβλίου, στο οποίο αναφέρεται μια σύντομη ιστορία, σαν «εκφώνηση». Σε αυτήν παρουσιάζεται ποιο είναι το επιθυμητό αποτέλεσμα ενός προγράμματος, τι στόχευε να κατασκευάζει ένα πρόγραμμα. Ωστόσο, το πρόγραμμα περιέχει ένα «προσεκτικά σχεδιασμένο λάθος» και κατασκευάζει κάτι ημιτελές ή κάτι «άλλο». Για να διορθωθεί χρειάζεται μια διερεύνηση σχετικά με τα μαθηματικά που εμπλέκονται (π.χ. παραλληλόγραμμα). Η διόρθωση δε γίνεται μόνο με έναν τρόπο. Η «εκφώνηση» απευθύνει στα παιδιά την πρόκληση να τροποποιήσουν/διορθώσουν το πρόγραμμα, ώστε να κατασκευάζει το επιθυμητό σχήμα.
Αρχικά, ο εκπαιδευτικός χωρίζει τους μαθητές σε ομάδες και τους αναθέτει ρόλους (ή τους ζητά να αναλάβουν ρόλους) χειριστή ψηφιακού εργαλείου, συντονιστή και χρήστη τετραδίου. Αυτό γίνεται κάθε φορά που αρχίζει νέα διδακτική ώρα. Στη συνέχεια του ζητά να ανοίξουν ένα μικροπείραμα, ξεκινώντας από το πρώτο και να το διαβάσουν, απαντώντας στο ζητούμενο. Σε καμία φάση του σεναρίου ο εκπαιδευτικός δεν συνοψίζει το ζητούμενο, αλλά αφήνει τα παιδιά να το συμπεράνουν από το κείμενο του μικροπειράματος. Αν μια ομάδα τελειώσει με κάποιο από τα μικροπειράματα και δεν υπάρχει κάτι σχετικό που να συζητείται στην ομάδα (π.χ. κάποια ανοικτή διερεύνηση) ή κάτι που να εκτιμά ο εκπαιδευτικός ότι χρειάζεται να συζητηθεί για την επίτευξη των προσδοκώμενων μαθησιακών αποτελεσμάτων, τότε τους αναθέτει το επόμενο μικροπείραμα (επόμενη φάση), χωρίς απαραίτητα να έχουν ολοκληρώσει τη διερεύνηση οι άλλες ομάδες.
Στη Φάση 1 του σεναρίου οι μαθητές κατασκευάζουν/διορθώνουν το πρόγραμμα ώστε να φτιάχνει τετράγωνο, ενώ στη Φάση 2 χρησιμοποιούν (σε άλλο μικροπείραμα) εντολές επανάληψης για την κατασκευή τετραγώνου. Στη Φάση 3 κατασκευάζουν/τροποποιούν το πρόγραμμα του μικροπειράματος, ώστε να φτιάχνει παραλληλόγραμμο με χρήση του συμβολισμού παραπληρωματικών γωνιών ενώ στη Φάση 4 σχεδιάζουν πρόγραμμα που να κατασκευάζει γενικευμένο παραλληλόγραμμο (με μεταβλητές πλευρές και γωνίες). Στη συνέχεια δημιουργούν σχήματα δικής τους έμπνευσης. Σε όλες τις φάσεις οι προκλήσεις απαντώνται μετά από διερεύνηση και οι μαθητές/τριες δημιουργούν μαθηματικά νοήματα καθώς προσπαθούν να τις αντιμετωπίσουν.
Η δομή της ροής του σεναρίου είναι αυτή που ακολουθεί (ο χρόνος που υπολογίζεται για κάθε φάση δίνεται ως ένα μέτρο σύγκρισης μεταξύ των φάσεων, τελείως ενδεικτικά).
«Μια διαδικασία που κατασκευάζει πάντοτε τετράγωνα»
Συνοπτική περιγραφήΒασίζεται στο ομώνυμο μικροπείραμα που βρίσκεται στον παρακάτω σύνδεσμο.
http://photodentro.edu.gr/v/item/ds/8521/9534
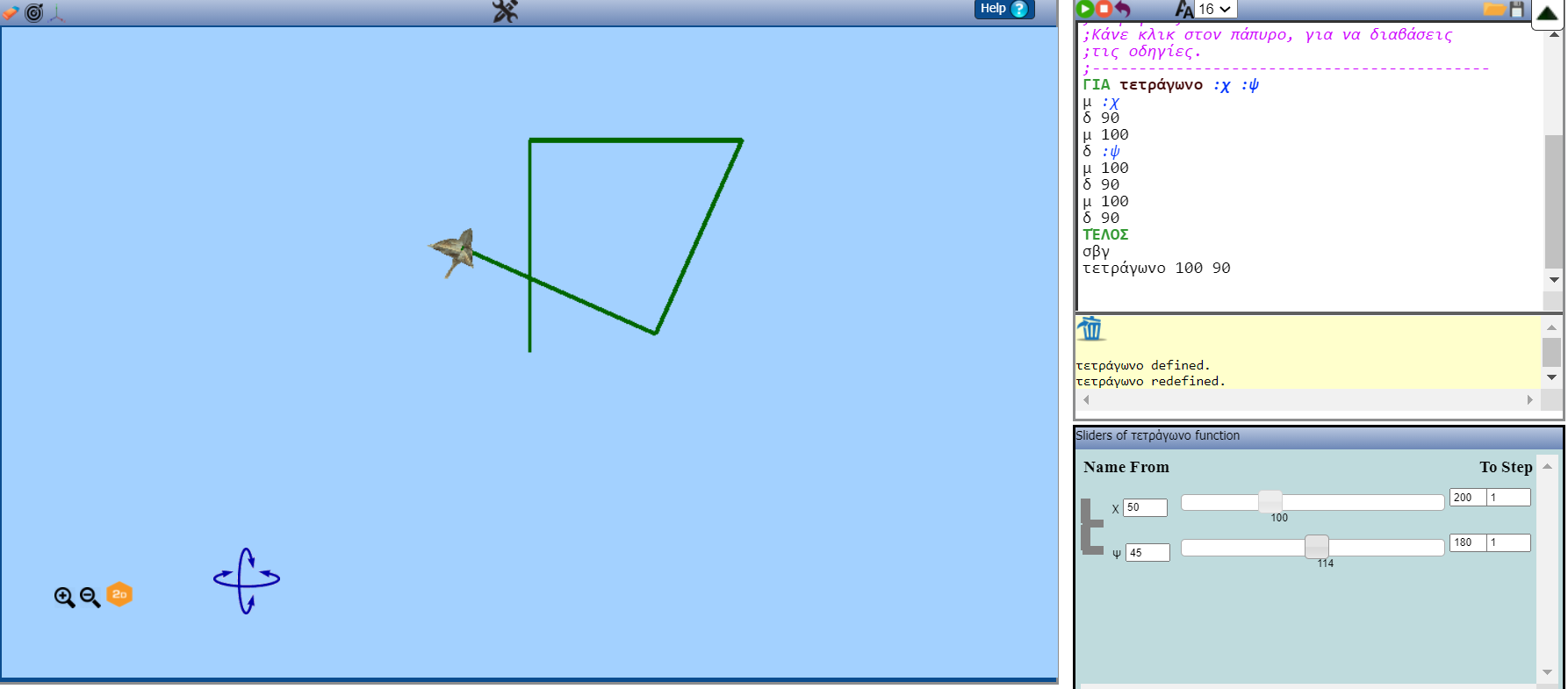
Το κείμενο του μικροπειράματος: «Η Δήμητρα έφτιαξε τη παρακάτω διαδικασία «τετράγωνο» για να κατασκευάσει ένα τετράγωνο. Το εκτέλεσε δίνοντας τις τιμές 100 για τη μεταβλητή :χ και 90 για την μεταβλητή :ψ. Όταν το εκτέλεσε όμως, διαπίστωσε ότι αν πειράξει τους μεταβολείς το τετράγωνο χαλάει. Μπορείς να βοηθήσεις τη Δήμητρα έτσι ώστε για κάθε τιμή των μεταβλητών να παραμένει τετράγωνο; Κάνε κλικ στον πάπυρο, για να διαβάσεις τις οδηγίες.
Το πρόγραμμα:
για τετράγωνo :χ :ψ
μ :χ
δ 90
μ 100
δ :ψ
μ 100
δ 90
μ 100
δ 90
τέλος
τετράγωνo 100 90
Για να αντιμετωπίσουν το ερώτημα, τα παιδιά, θα χρειαστεί να χρησιμοποιήσουν μόνο μια μεταβλητή και όχι δύο.
Διδακτικοί στόχοι / Προσδοκώμενα μαθησιακά αποτελέσματα>> Χρησιμοποιούν την ίδια μεταβλητή για να εκφράσουν ότι θα πρέπει δύο ή περισσότερες ποσότητες να είναι ίσες.
>> Κατασκευάζουν στη Χελωνόσφαιρα γενικευμένο τετράγωνο.
>> Εξηγούν γιατί έχουν χρησιμοποιήσει μεταβλητές, με συγκεκριμένο τρόπο, σε κάθε ένα από τα παραπάνω προγράμματα.
>> Συνδέουν τη χρήση των μεταβλητών στα προγράμματα με τις ιδιότητες του τετραγώνου.
>> Αξιολογούν τα προγράμματα των συμμαθητών τους.
>> Διερευνούν διαφορετικές περιπτώσεις, ώστε να αντιμετωπίσουν το ερώτημα που τους τίθεται από το έργο.
>> Πειραματίζονται στη Χελωνόσφαιρα για να πετύχουν τις κατασκευές που ζητούνται.
>> Κάνουν εικασίες και υποθέσεις τις οποίες ελέγχουν στο περιβάλλον της Χελωνόσφαιρας.
>> Θέτουν επιμέρους ερωτήματα για να πετύχουν το ζητούμενο.
>> Θέτουν σχετικά ερωτήματα δικού τους ενδιαφέροντος.
>> Παίρνουν αποφάσεις ως προς τη λύση που θα παρουσιάσουν ανάμεσα στις προτεινόμενες στην ομάδα τους.
>> Τεκμηριώνουν τις επιλογές τους σε συζήτηση στην ολομέλεια.
>> Δείχνουν ανοχή στην αμφισημία.
>> Αναζητούν λύση ακολουθώντας τη «κουλτούρα του δημιουργού».
>> Καταβάλουν προσπάθεια για συναινέσεις στην ομάδα.
Είδος δραστηριότηταςΕίναι η πρώτη πρόκληση στο πλαίσιο του σεναρίου και έτσι ενδέχεται να γίνουν τα εξής:
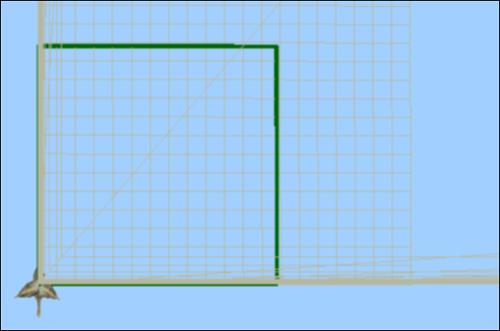
>> Τα παιδιά θα προτείνουν τιμές των :χ και :ψ, που θα ανακαλύψουν με τη χρήση των μεταβολέων, για τις οποίες το σχήμα είναι τετράγωνο. Ο εκπαιδευτικός μπορεί να το χρησιμοποιήσει ως ευκαιρία για κατανοήσουν τα παιδιά τι σημαίνει «γενικευμένο τετράγωνο», δηλαδή ένα σχήμα που αν και μεταβάλλεται παραμένει τετράγωνο, όπως στο παρακάτω σχήμα.
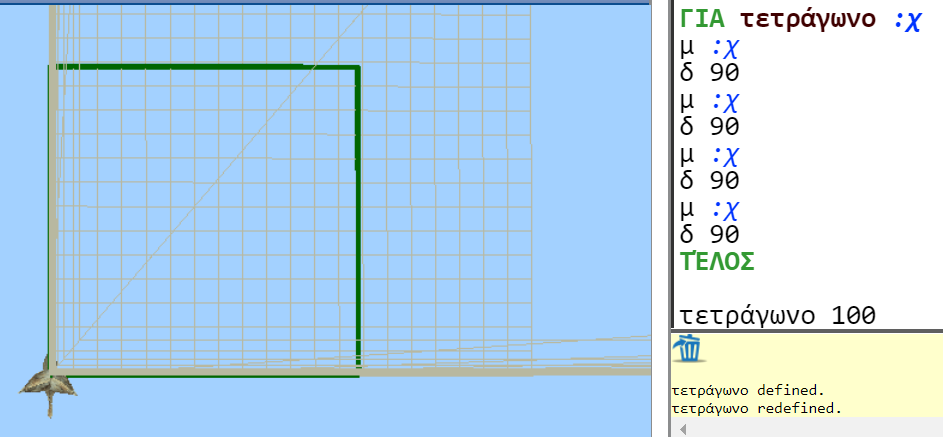
Μπορεί να «χαλάσει» το σχήμα των παιδιών με χρήση του μεταβολέα και να ζητήσει να το φτιάξουν ώστε «να μεταβάλλεται, αλλά να παραμένει τετράγωνο. Τα σχήματα που ζητούνται και στις επόμενες φάσεις του σεναρίου είναι γενικευμένα, άρα αν αξιοποιηθεί αυτή η ευκαιρία θα είναι χρήσιμη και παρακάτω.
Υπενθυμίζεται οι μαθητές/τριες δουλεύουν σε ομάδες όπως έχει ήδη περιγραφεί.
>> Ενδέχεται κάποια ομάδα παιδιών να φτιάξουν ένα πρόγραμμα χωρίς μεταβλητές, που να σχεδιάζει τετράγωνο. Αυτό είναι άλλη μια ευκαιρία για να επισημάνει ο εκπαιδευτικός «τι ζητείται» (ένα γενικευμένο τετράγωνο). Αν μια άλλη ομάδα έχει φτιάξει γενικευμένο τετράγωνο, ιδανικό είναι να προκληθεί από τον εκπαιδευτικό επικοινωνία μεταξύ των δύο ομάδων αυτών, με στόχο την ανταλλαγή ιδεών, την ετερο-αξιολόγησή τους, την τεκμηρίωση των επιλογών τους, κτλ.
Εκτιμώμενη διάρκεια1 διδακτική ώρα
Τεχνική/ές διδασκαλίαςΙσχύουν τα αναφερόμενα στην παράγραφο «Παιδαγωγική προσέγγιση και στρατηγικές».
Επιπροσθέτως εξειδικεύεται ότι, ίσως χρειαστεί σε αυτό το σημείο περισσότερο η επισήμανση για τη χρησιμότητα των μεταβλητών, χωρίς καθοδήγηση, γιατί είναι η πρώτη πρόκληση στην οποία εμπλέκονται τα παιδιά, σε αυτό το σενάριο.
ΕργαλείαΧελωνόσφαιρα
«Γίνεται η διαδικασία να κατασκευάζει πάντα τετράγωνα;»
Συνοπτική περιγραφήΒασίζεται στο ομώνυμο μικροπείραμα που βρίσκεται στον παρακάτω σύνδεσμο.
http://photodentro.edu.gr/v/item/ds/8521/9524
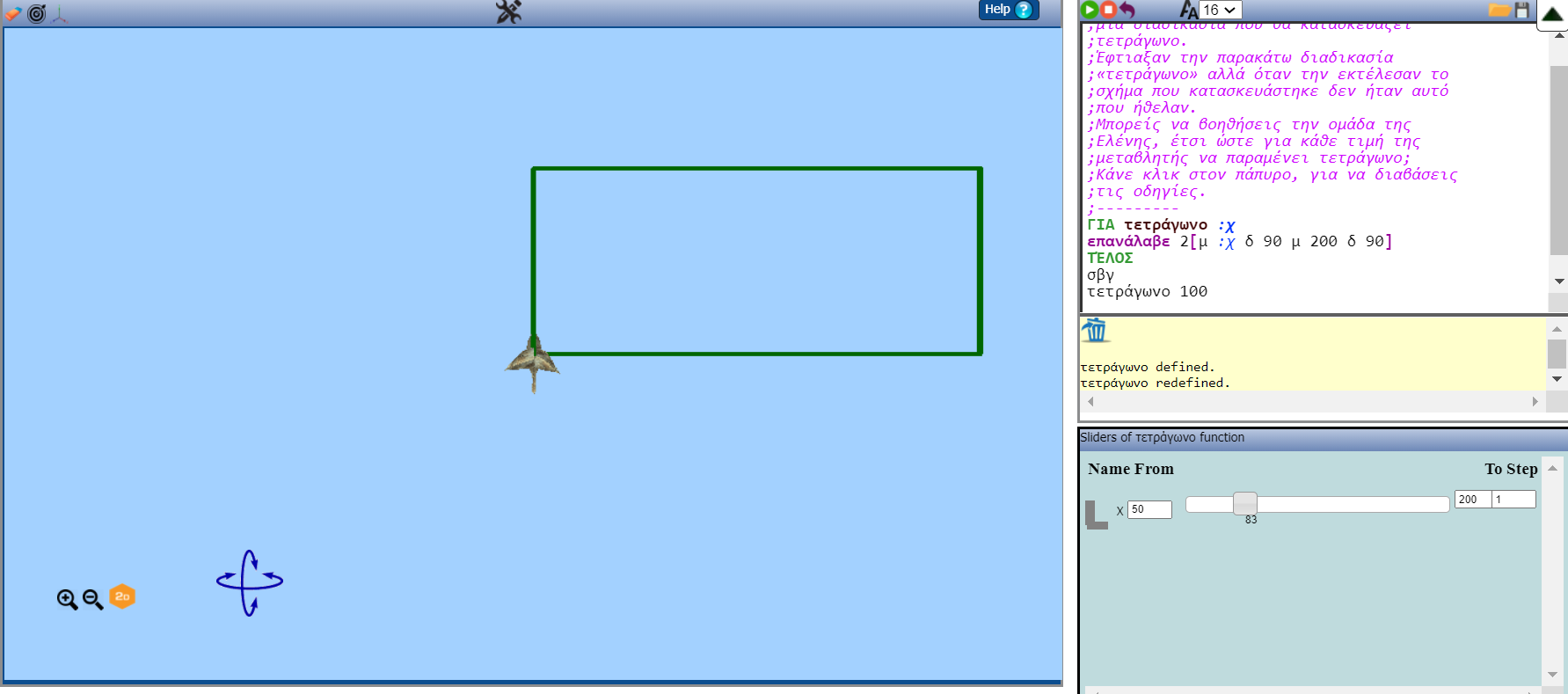
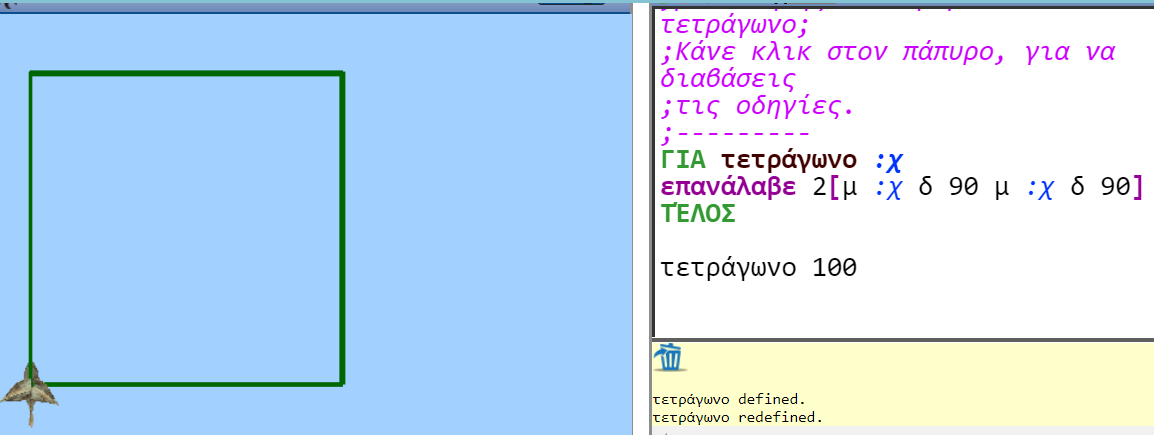
Το κείμενο του μικροπειράματος: «Η ομάδα της Ελένης προσπάθησε να φτιάξει μία διαδικασία που θα κατασκευάζει τετράγωνο. Έφτιαξαν την παρακάτω διαδικασία «τετράγωνο» αλλά όταν την εκτέλεσαν το σχήμα που κατασκευάστηκε δεν ήταν αυτό που ήθελαν. Μπορείς να βοηθήσεις την ομάδα της Ελένης, έτσι ώστε για κάθε τιμή της μεταβλητής να παραμένει τετράγωνο; Κάνε κλικ στον πάπυρο, για να διαβάσεις τις οδηγίες.»
Το πρόγραμμα:
για τετράγωνο :χ
επανάλαβε 2[μ :χ δ 90 μ 200 δ 90]
τέλος
τετράγωνο 100
Στόχος είναι να τροποποιηθεί το πρόγραμμα, όπως φαίνεται στην παρακάτω εικόνα.
>> Χρησιμοποιούν την ίδια μεταβλητή για να εκφράσουν ότι θα πρέπει δύο ή περισσότερες ποσότητες να είναι ίσες.
>> Κατασκευάζουν στη Χελωνόσφαιρα γενικευμένο τετράγωνο και παραλληλόγραμμο.
>> Αναγνωρίζουν μοτίβα στην κατασκευή του τετραγώνου (π.χ. πηγαίνεις μπροστά :χ και δεξιά 90, 4 φορές) και του παραλληλογράμμου.
>> Χρησιμοποιούν αυτά τα μοτίβα στην κατασκευή τετραγώνου και παραλληλογράμμου, με εντολές επανάληψης.
>> Ανακαλούν στρατηγικές κατασκευής σχημάτων και τις χρησιμοποιούν σε άλλες κατηγορίες σχημάτων.
>> Εξηγούν γιατί έχουν χρησιμοποιήσει μεταβλητές, με συγκεκριμένο τρόπο, σε κάθε ένα από τα παραπάνω προγράμματα.
>> Συνδέουν τη χρήση των μεταβλητών στα προγράμματα με τις ιδιότητες του τετραγώνου και του παραλληλογράμμου.
>> Αξιολογούν τα προγράμματα των συμμαθητών τους.
>> Διερευνούν διαφορετικές περιπτώσεις, ώστε να αντιμετωπίσουν το ερώτημα που τους τίθεται από το έργο.
>> Πειραματίζονται στη Χελωνόσφαιρα για να πετύχουν τις κατασκευές που ζητούνται.
>> Κάνουν εικασίες και υποθέσεις τις οποίες ελέγχουν στο περιβάλλον της Χελωνόσφαιρας.
>> Θέτουν επιμέρους ερωτήματα για να πετύχουν το ζητούμενο.
>> Θέτουν σχετικά ερωτήματα δικού τους ενδιαφέροντος.
>> Παίρνουν αποφάσεις ως προς τη λύση που θα παρουσιάσουν ανάμεσα στις προτεινόμενες στην ομάδα τους.
>> Τεκμηριώνουν τις επιλογές τους σε συζήτηση στην ολομέλεια.
>> Δείχνουν ανοχή στην αμφισημία.
>> Αναζητούν λύση ακολουθώντας τη «κουλτούρα του δημιουργού».
>> Καταβάλουν προσπάθεια για συναινέσεις στην ομάδα.
Είδος δραστηριότηταςΜε το πρόγραμμα που τροποποιούν σε αυτό το μικροπείραμα οι μαθητές και οι μαθήτριες κατασκευάζουν ένα γενικευμένο τετράγωνο με τη χρήση εντολών επανάληψης. Έτσι, εκφράζουν συμβολικά, με γλώσσα προγραμματισμού, μοτίβα που υπάρχουν στο σχήμα (πλευρά μήκος :χ-ορθή γωνία-πλευρά μήκος :χ-ορθή γωνία). Τέτοια μοτίβα θα χρησιμοποιήσουν και σε επόμενη φάση του σεναρίου.
Στη συνέχεια, προτείνεται στον εκπαιδευτικό να θέσει τα παρακάτω ερωτήματα, ως επέκταση του μικροπειράματος:
>> «Μπορείτε να κατασκευάσετε το τετράγωνο, με χρήση επανάληψης, αλλιώς;
Θα μπορούσαν να αναζητήσουν τη χρήση άλλου μοτίβου όπως «πλευρά μήκος :χ-ορθή γωνία», 4 φορές.
>> «Μπορείτε να κατασκευάσετε ορθογώνιο με χρήση επανάληψης;
Εκτιμώμενη διάρκεια1 διδακτική ώρα
Τεχνική/ές διδασκαλίαςΙσχύουν τα αναφερόμενα στην παράγραφο «Παιδαγωγική προσέγγιση και στρατηγικές».
Επιπροσθέτως εξειδικεύεται ότι, ο εκπαιδευτικός θα πρέπει να είναι σε ετοιμότητα να ανταποκριθεί σε ανάγκες διαφοροποιημένης διδασκαλίας, π.χ. όταν μια ομάδα μαθητών ή ένας μαθητής/τρια προτείνει εναλλακτικό τρόπο κατασκευής του σχήματος (χρήση επανάληψης με άλλο τρόπο, κτλ). Θα πρέπει να κρίνει αν θα υποστηρίξει το μαθητή/τη μαθήτρια να συνεχίσει αυτόνομα και στη συνέχεια να προκαλέσει την επικοινωνία του με τους υπόλοιπους, ή αν θα το κάνει εκείνη τη στιγμή, κτλ.
ΕργαλείαΧελωνόσφαιρα
«Οι απέναντι γωνίες του παραλληλογράμμου»
Συνοπτική περιγραφήΒασίζεται στο ομώνυμο μικροπείραμα που βρίσκεται στον παρακάτω σύνδεσμο.
http://photodentro.edu.gr/v/item/ds/8521/9545

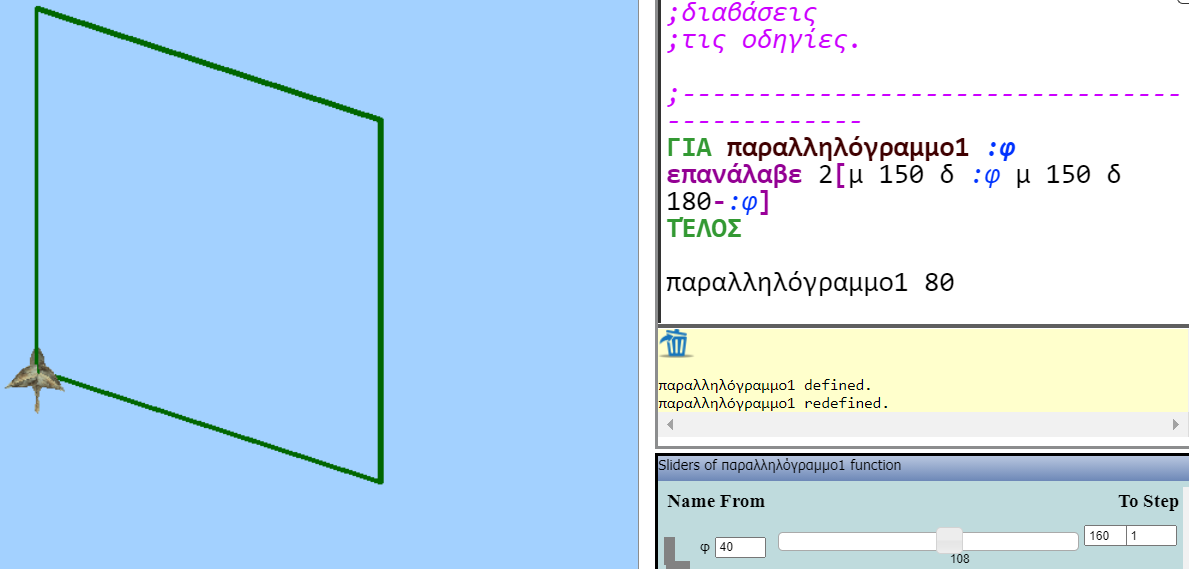
Το κείμενο του μικροπειράματος: «Ο Νίκος έφτιαξε τη διαδικασία «παραλληλόγραμμο1», έτσι ώστε η οντότητα να κατασκευάζει παραλληλόγραμμα με πλευρές 100 και 150. Όταν εκτέλεσε τη διαδικασία «παραλληλόγραμμο1 80 80» παρατήρησε ότι δεν σχηματίστηκε παραλληλόγραμμο. Μπορείς να βοηθήσεις το Νίκο έτσι ώστε, να κατασκευάζεται πάντα παραλληλόγραμμο όταν εκτελεί τη διαδικασία; Κάνε κλικ στον πάπυρο, για να διαβάσεις τις οδηγίες.»
Το πρόγραμμα:
για παραλληλόγραμμο1 :φ :ω
επανάλαβε 2[μ 100 δ :φ μ 150 δ :ω]
τέλος
παραλληλόγραμμο1 80 80
Στο παρακάτω σχήμα φαίνεται μια κατασκευή και το αντίστοιχο πρόγραμμα, πιθανή απάντηση στο μικροπείραμα.
>> Χρησιμοποιούν μεταβλητές για να εκφράσουν σχέσεις εξάρτησης, όπως της παραπληρωματικής γωνίας (180-φ).
>> Κατασκευάζουν στη Χελωνόσφαιρα γενικευμένο παραλληλόγραμμο.
>> Αναγνωρίζουν μοτίβα στην κατασκευή του παραλληλογράμμου.
>> Χρησιμοποιούν αυτά τα μοτίβα στην κατασκευή παραλληλογράμμου, με εντολές επανάληψης.
>> Χρησιμοποιούν την έκφραση 180-φ, για να σχεδιάσουν τα παραπάνω σχήματα.
>> Ανακαλούν στρατηγικές κατασκευής σχημάτων και τις χρησιμοποιούν σε άλλες κατηγορίες σχημάτων.
>> Εξηγούν γιατί έχουν χρησιμοποιήσει μεταβλητές, με συγκεκριμένο τρόπο, σε κάθε ένα από τα παραπάνω προγράμματα.
>> Συνδέουν τη χρήση των μεταβλητών στα προγράμματα με τις ιδιότητες του παραλληλογράμμου.
>> Αξιολογούν τα προγράμματα των συμμαθητών τους.
>> Διερευνούν διαφορετικές περιπτώσεις, ώστε να αντιμετωπίσουν το ερώτημα που τους τίθεται από το έργο.
>> Πειραματίζονται στη Χελωνόσφαιρα για να πετύχουν τις κατασκευές που ζητούνται.
>> Κάνουν εικασίες και υποθέσεις τις οποίες ελέγχουν στο περιβάλλον της Χελωνόσφαιρας.
>> Θέτουν επιμέρους ερωτήματα για να πετύχουν το ζητούμενο.
>> Θέτουν σχετικά ερωτήματα δικού τους ενδιαφέροντος.
>> Παίρνουν αποφάσεις ως προς τη λύση που θα παρουσιάσουν ανάμεσα στις προτεινόμενες στην ομάδα τους.
>> Τεκμηριώνουν τις επιλογές τους σε συζήτηση στην ολομέλεια.
>> Δείχνουν ανοχή στην αμφισημία.
>> Αναζητούν λύση ακολουθώντας τη «κουλτούρα του δημιουργού».
>> Καταβάλουν προσπάθεια για συναινέσεις στην ομάδα.
Είδος δραστηριότηταςΜε την κατασκευή αυτή, ή άλλες που απαντούν στην πρόκληση του μικροπειράματος, οι μαθητές χρησιμοποιούν την έκφραση 180-:φ, ώστε να συμβολίσουν τη σχέση εξάρτησης μεταξύ δύο διαδοχικών στροφών της οντότητας (στη Χελωνόσφαιρα) και αντιστοιχούν στην ιδιότητα του παραλληλογράμμου, οι διαδοχικές γωνίες του να είναι παραπληρωματικές. Ο ρόλος του εκπαιδευτικού είναι να εξασφαλίσει την ευκαιρία στους μαθητές και τις μαθήτριες, να φτάσουν σε στη συμβολική έκφραση της παραπληρωματικής γωνίας και τη χρήση της μέσα από διερεύνηση και χωρίς να προδιαγράψει την πορεία αυτή. Δεν είναι αυτονόητο ότι τα παιδιά θα χρησιμοποιήσουν άμεσα μια τέτοια έκφραση στο πρόγραμμα. Θα πρέπει να έχουν το χρόνο να πειραματιστούν, να δοκιμάσουν αλγεβρικές εκφράσεις στο πρόγραμμα και να συνεργαστούν για να το πετύχουν. Επίσης, δεν είναι αυτονόητο ότι πρώτα θα εκφράσουν αλγεβρικά την παραπληρωματική γωνία της :φ, ως 180-:φ και στη συνέχεια θα τη χρησιμοποιήσουν στο πρόγραμμα. Άρα, είναι επωφελές να έχουν το χρόνο να αλληλεπιδράσουν μεταξύ τους και με το ψηφιακό εργαλείο, για να αναπτύξουν στρατηγικές, ώστε να το πετύχουν, δημιουργώντας νοήματα για τον αλγεβρικό συμβολισμό, την έννοια της μεταβλητής, κτλ.
Επισημαίνεται ότι οι μαθητές/τριες ενδεχομένως να κατασκευάσουν ένα ορθογώνιο, χρησιμοποιώντας την εντολή δεξιά 90 και αφαιρώντας τις μεταβλητές :φ και :ω από το «δεξιά». Τότε, ο εκπαιδευτικός κουνάει τους μεταβολείς και τους προκαλεί να κατασκευάσουν ένα παραλληλόγραμμο που να μπορεί να είναι και πλάγιο.
Εκτιμώμενη διάρκεια1-2 διδακτικές ώρες
Τεχνική/ές διδασκαλίαςΙσχύουν τα αναφερόμενα στην παράγραφο «Παιδαγωγική προσέγγιση και στρατηγικές».
Επιπροσθέτως εξειδικεύεται ότι είναι χρήσιμο να υπάρχει διαθέσιμος χρόνος για διερεύνηση από τους μαθητές/τριες. Ο συμβολισμός 180-:φ, των παραπληρωματικών γωνιών, είναι αρκετά αφαιρετικός, δεν είναι αυτονόητος, όπως δεν είναι αυτονόητη και η χρήση του. Η πορεία που θα ακολουθήσουν για να τον χρησιμοποιήσουν δεν μπορεί να προβλεφθεί. Άρα, είναι σκόπιμο να έχουν, τα παιδιά, χρόνο για επικοινωνία μεταξύ τους και αλληλεπίδραση με το ψηφιακό εργαλείο (πειραματισμός, ανατροφοδότηση, κτλ). Ο εκπαιδευτικός, εκτός από την μέριμνα για τα παραπάνω, χρειάζεται και να παρατηρεί τις συζητήσεις των ομάδων, ώστε να φέρει στην ολομέλεια ή στις ομάδες στοιχεία που θα βοηθήσουν τη διερεύνηση, χωρίς να την καθοδηγήσουν σε σημαντικό βαθμό.
ΕργαλείαΧελωνόσφαιρα
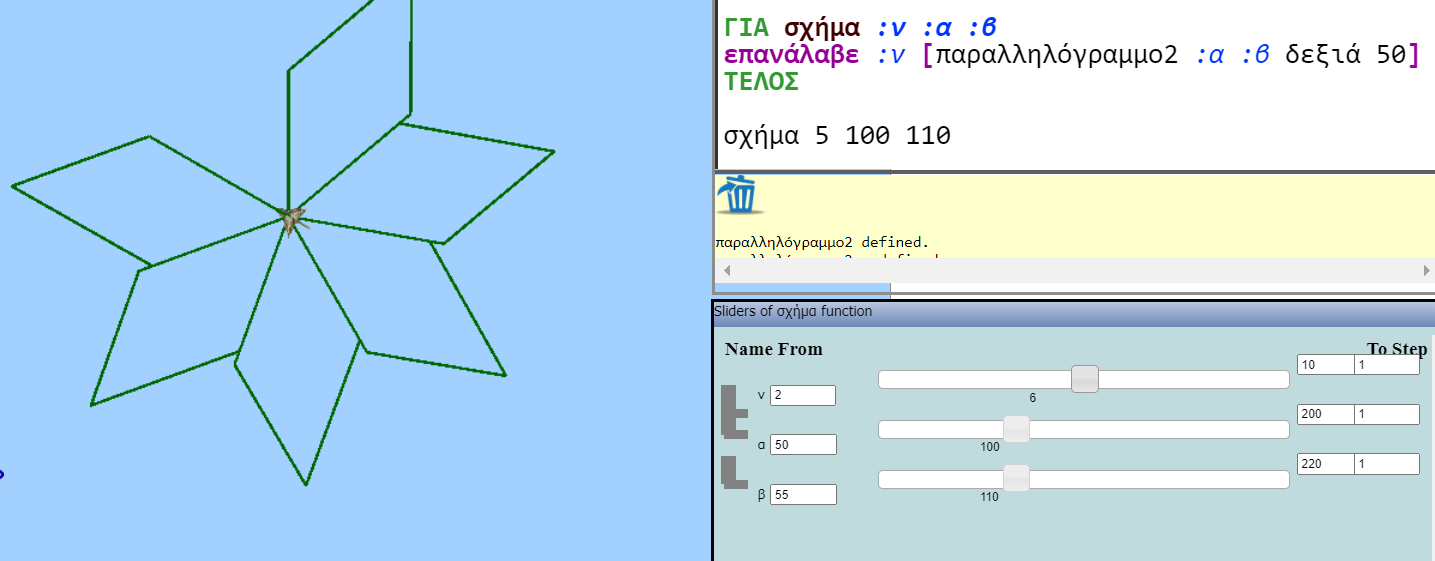
Κατασκευή γενικευμένου παραλληλογράμμου και οι δικές σας κατασκευές
Συνοπτική περιγραφήΜε βάση το μικροπείραμα «Ποια είναι η σχέση μεταξύ των απέναντι πλευρών παραλληλογράμμου;»
http://photodentro.edu.gr/v/item/ds/8521/9528
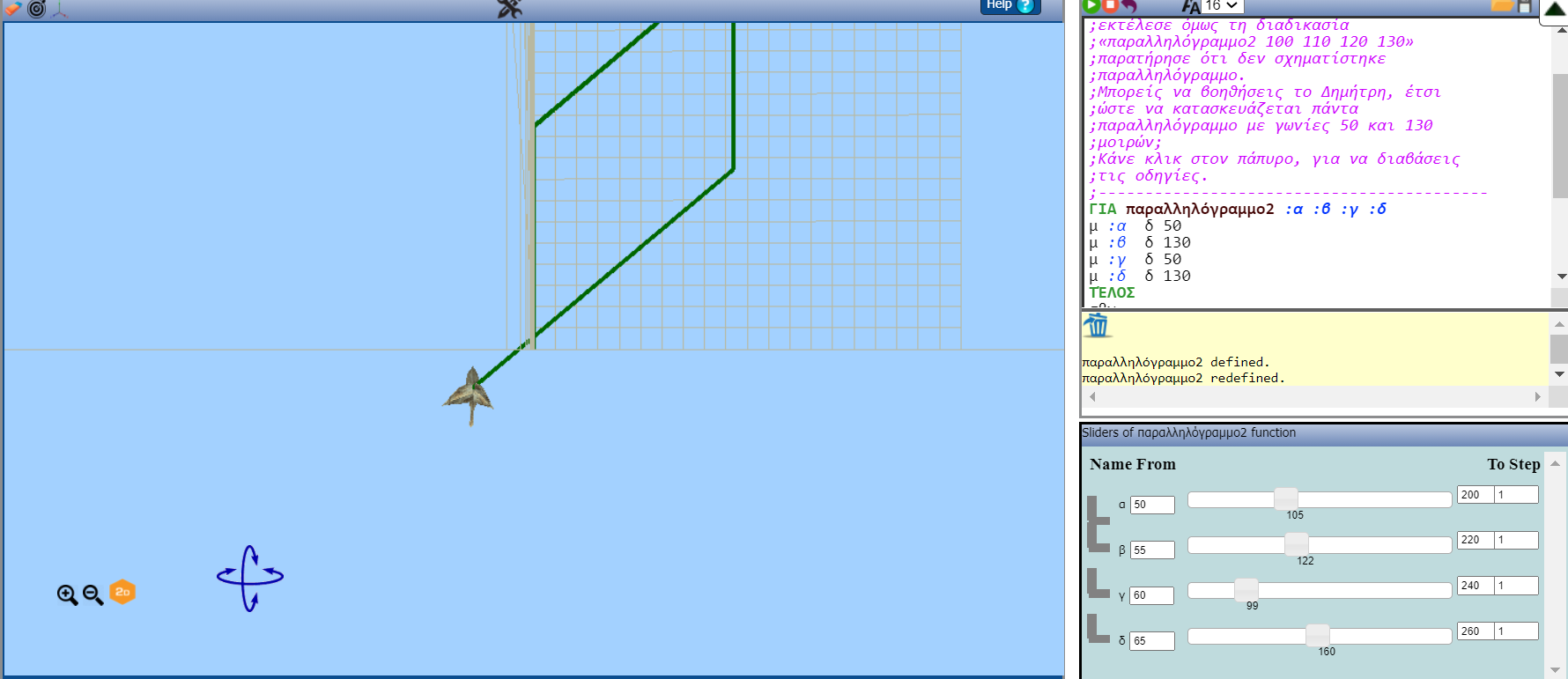
Το κείμενο του μικροπειράματος: «Ο Δημήτρης έφτιαξε τη διαδικασία «παραλληλόγραμμο2», έτσι ώστε η οντότητα να κατασκευάζει παραλληλόγραμμα με γωνίες 50 και 130 μοιρών. Όταν εκτέλεσε όμως τη διαδικασία «παραλληλόγραμμο2 100 110 120 130» παρατήρησε ότι δεν σχηματίστηκε παραλληλόγραμμο. Μπορείς να βοηθήσεις το Δημήτρη, έτσι ώστε να κατασκευάζεται πάντα παραλληλόγραμμο με γωνίες 50 και 130 μοιρών; Κάνε κλικ στον πάπυρο, για να διαβάσεις τις οδηγίες.»
Το πρόγραμμα:
για παραλληλόγραμμο2 :α :β :γ :δ
μ :α δ 50
μ :β δ 130
μ :γ δ 50
μ :δ δ 130
τέλος
παραλληλόγραμμο2 100 110 120 130
Ένας πιθανός τρόπος να απαντηθεί η πρόκληση, φαίνεται στο παρακάτω σχήμα.
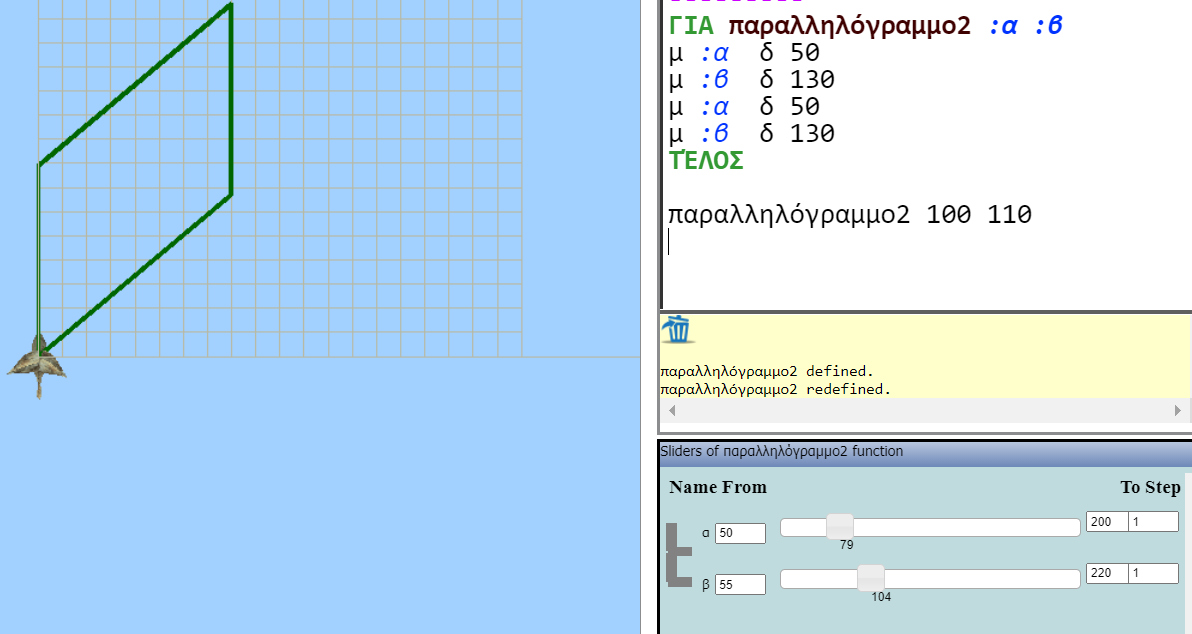
Στη συνέχεια ζητείται από τα παιδιά, συνεχίζοντας στις ομάδες τους, να φτιάξουν κατασκευές δικής τους έμπνευσης, χρησιμοποιώντας ό,τι έχουν κατασκευάσει στις προηγούμενες φάσεις.
Διδακτικοί στόχοι / Προσδοκώμενα μαθησιακά αποτελέσματα>> Χρησιμοποιούν την ίδια μεταβλητή για να εκφράσουν ότι θα πρέπει δύο ή περισσότερες ποσότητες να είναι ίσες.
>> Χρησιμοποιούν μεταβλητές για να εκφράσουν σχέσεις εξάρτησης, όπως της παραπληρωματικής γωνίας (180-φ).
>> Κατασκευάζουν στη Χελωνόσφαιρα γενικευμένο παραλληλόγραμμο.
>> Αναγνωρίζουν μοτίβα στην κατασκευή του παραλληλογράμμου.
>> Χρησιμοποιούν αυτά τα μοτίβα στην κατασκευή παραλληλογράμμου, με εντολές επανάληψης.
>> Χρησιμοποιούν την έκφραση 180-φ, για να σχεδιάσουν τα παραπάνω σχήματα.
>> Ανακαλούν στρατηγικές κατασκευής σχημάτων και τις χρησιμοποιούν σε άλλες κατηγορίες σχημάτων.
>> Εξηγούν γιατί έχουν χρησιμοποιήσει μεταβλητές, με συγκεκριμένο τρόπο, σε κάθε ένα από τα παραπάνω προγράμματα.
>> Αξιολογούν τα προγράμματα των συμμαθητών τους.
>> Δημιουργούν δικά τους σχήματα με δομικές λίθους τα προγράμματα τετραγώνου, παραλληλογράμμου που έχουν ήδη κατασκευάσει.
>> Διερευνούν διαφορετικές περιπτώσεις, ώστε να αντιμετωπίσουν το ερώτημα που τους τίθεται από το έργο.
>> Πειραματίζονται στη Χελωνόσφαιρα για να πετύχουν τις κατασκευές που ζητούνται.
>> Κάνουν εικασίες και υποθέσεις τις οποίες ελέγχουν στο περιβάλλον της Χελωνόσφαιρας.
>> Θέτουν επιμέρους ερωτήματα για να πετύχουν το ζητούμενο.
>> Θέτουν σχετικά ερωτήματα δικού τους ενδιαφέροντος.
>> Παίρνουν αποφάσεις ως προς τη λύση που θα παρουσιάσουν ανάμεσα στις προτεινόμενες στην ομάδα τους.
>> Τεκμηριώνουν τις επιλογές τους σε συζήτηση στην ολομέλεια.
>> Δείχνουν ανοχή στην αμφισημία.
>> Αναζητούν λύση ακολουθώντας τη «κουλτούρα του δημιουργού».
>> Καταβάλουν προσπάθεια για συναινέσεις στην ομάδα.
Είδος δραστηριότηταςΕδώ, το μικροπείραμα είναι εστιασμένο στην χρήση συμβολικής έκφρασης για την ιδιότητα των παραλληλογράμμων να έχουν τις μη διαδοχικές πλευρές τους ίσες. Ενδέχεται ομάδες μαθητών να χρησιμοποιήσουν εντολές επανάληψης. Είναι χρήσιμο, ο εκπαιδευτικός να δώσει ευκαιρίες επικοινωνίας, συζήτησης και αξιολόγησης διαφορετικών στρατηγικών, μεταξύ των ομάδων.
Προτείνεται, στη συνέχεια, να τεθούν ερωτήματα στα παιδιά όπως:
>> Θα μπορούσατε να κατασκευάσετε ένα παραλληλόγραμμο με μεταβλητές πλευρές και γωνίες;
Εδώ, στόχος είναι να ανακαλέσουν τη χρήση της συμβολικής έκφρασης 180-:φ από την προηγούμενη φάση, για να τη χρησιμοποιήσουν.
>> Μπορείτε να κατασκευάσετε ένα σχήμα της επιλογής σας με βάση αυτά που έχετε κάνει ως τώρα;
Με αυτό το ερώτημα, τα παιδιά θα θέσουν τα ίδια, όχι μόνο τα επιμέρους ερωτήματα, αλλά και το κεντρικό ερώτημα της διερεύνησής τους και έτσι η διερεύνηση θα έχει μεγαλύτερη αξία για τα ίδια και θα τα αφορά περισσότερο. Ίσως είναι χρήσιμο, ο εκπαιδευτικός να δώσει στα παιδιά παραδείγματα, χωρίς να τα περιορίσει. Τέτοια παραδείγματα μπορεί να είναι ένα σχήμα που να θυμίζει ανεμόμυλο, ένα πλακόστρωτο πάτωμα, κτλ.
Στο παρακάτω σχήμα φαίνεται μια τέτοια κατασκευή. Ανάλογα με τις πρώτες κατασκευές των παιδιών, μπορεί ο εκπαιδευτικός να θέτει επιπλέον ερωτήματα, όπως «Πώς γίνεται να κλείσει σωστά το παρακάτω σχήμα;» ή «πώς μπορεί να μεταβάλλεται το πλήθος των παραλληλογράμμων και να κλείνει το σχήμα;», κτλ.
2 διδακτικές ώρες
Τεχνική/ές διδασκαλίαςΓια να επιτευχθούν τα προσδοκώμενα μαθησιακά αποτελέσματα ακολουθείται η προσέγγιση του Constructionism, της μάθησης μέσα από το μαστόρεμα, που δίνει την ευκαιρία στα παιδιά να δημιουργήσουν νοήματα προσπαθώντας να πετύχουν κάτι που έχει αξία για τα ίδια. Η πρόκληση ξεκινάει από συγκεκριμένα μικροπειράματα που θέτουν το σχετικό μαθηματικό περικείμενο, καθώς είναι εστιασμένα. Από την άλλη τα ερωτήματα που τίθενται μπορούν να απαντηθούν με διαφορετικούς τρόπους. Έτσι, τα παιδιά θέτουν τα ίδια επιμέρους ερωτήματα και μαθαίνουν να διερευνούν και να ψάχνουν λύσεις, να κάνουν υποθέσεις και εικασίες χωρίς να είναι μονοσήμαντα ορισμένο το επόμενο βήμα.
Για να απαντήσουν στα ερωτήματα που τίθενται από το έργο ή θέτουν τα παιδιά, θα χρειαστεί να χρησιμοποιήσουν μεταβλητές για να εκφράσουν συγκεκριμένες ιδιότητες. Ο ρόλος του εκπαιδευτικού είναι να επισημάνει τη χρησιμότητα των μεταβλητών, χωρίς να καθοδηγήσει τα παιδιά, ώστε τα ίδια να αναγνωρίζουν μοτίβα, ιδιότητες, κτλ και να πειραματιστούν με τη χρήση των αλγεβρικών εκφράσεων σε κάθε πρόγραμμα. Από την εκτέλεση των προγραμμάτων θα αποφανθούν αν χρειάζεται να αλλάξουν κάτι (κουλτούρα δημιουργού). Σε αυτό το σημείο οι λειτουργικότητες του ψηφιακού εργαλείου, οι σύνδεση μεταξύ δυναμικών αναπαραστάσεων (η χρήση των μεταβολέων), η ανατροφοδότηση που παρέχει στα παιδιά (εκτελούν το πρόγραμμα και βλέπουν τι συμβαίνει) είναι παράμετροι που υποστηρίζουν τον πειραματισμό, τη διερεύνηση και την κουλτούρα του δημιουργού. Επίσης, κρίσιμος είναι ο ρόλος του εκπαιδευτικού στην ενίσχυση, οργάνωση και διευκόλυνση της επικοινωνίας μεταξύ των παιδιών της ίδιας ομάδας ή στην ολομέλεια. Η επικοινωνία αυτή είναι αναγκαία ώστε να πάρουν αποφάσεις εντός της ομάδας, να διασφαλίσουν την συναίνεση εντός της ομάδας για να προχωρήσουν, να εξηγήσουν τις επιμέρους επιλογές τους, να τεκμηριώσουν τη στρατηγική που ακολούθησαν, να αξιολογήσουν τις προσπάθειες των συμμαθητών τους, να συνδέσουν τη μαθηματική γνώση με τις πρακτικές τους.
ΕργαλείαΧελωνόσφαιρα
Για την εφαρμογή του σεναρίου σε μεγαλύτερες τάξεις του Γυμνασίου δε χρειάζονται τροποποιήσεις. Προτείνεται μια επιπλέον πρόκληση/ερώτηση: «Μπορείτε να σχεδιάσετε ένα ορθογώνιο που να μην είναι τετράγωνο;»
Στόχος του επιπλέον ερωτήματος είναι να εμπλέξει τους μαθητές σε μια διερεύνηση που ενδεχομένως να θέσουν σε χρήση μια γραμμική σχέση μεταξύ των πλευρών, π.χ. αν :χ είναι το μήκος της μιας πλευράς, το μήκος της άλλης είναι :χ+10 (ή ένας άλλος θετικός αριθμός).
Η διδακτική προσέγγιση προτείνεται να είναι συμβατή με του παρόντος σεναρίου.
Για την αποτίμηση του σεναρίου προτείνεται ο εκπαιδευτικός να κρατάει σημειώσεις που, εκτός από τη φάση της αξιολόγησης, θα τον βοηθήσουν να παρακολουθήσει τη διδασκαλία και την πορεία της μάθησης και να επανασχεδιάζει κατά τη διάρκεια της εφαρμογής, από φάση σε φάση του σεναρίου.
Συνοδευτικό υλικό
| Όνομα αρχείου | Περιγραφή | Τύπος αρχείου | Μέγεθος αρχείου |
|---|---|---|---|
| Picture1.png | Εικόνα 1 | image/png | 90 KB |
| Picture2.png | Εικόνα 2 | image/png | 51 KB |
| Picture3.png | Εικόνα 3 | image/png | 98 KB |
| Picture4.png | Εικόνα 4 | image/png | 48 KB |
| Picture5.png | Εικόνα 5 | image/png | 110 KB |
| Picture6.png | Εικόνα 6 | image/png | 64 KB |
| Picture7.png | Εικόνα 7 | image/png | 121 KB |
| Picture8.png | Εικόνα 8 | image/png | 70 KB |
| Picture9.png | Εικόνα 9 | image/png | 82 KB |